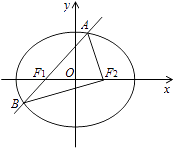题目内容
【题目】选修4-4:坐标系与参数方程
已知直线![]() 的参数方程为
的参数方程为![]() (
(![]() ,
, ![]() 为参数),曲线
为参数),曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)将曲线![]() 的极坐标方程化为直坐标方程,并说明曲线
的极坐标方程化为直坐标方程,并说明曲线![]() 的形状;
的形状;
(2)若直线![]() 经过点
经过点![]() ,求直线
,求直线![]() 被曲线
被曲线![]() 截得的线段
截得的线段![]() 的长.
的长.
【答案】(1)详见解析;(2)8.
【解析】试题分析:(1)将曲线![]() 的极坐标方程为
的极坐标方程为![]() 两边同时乘以
两边同时乘以![]() ,利用极坐标与直角坐标之间的关系即可得出其直角坐标方程;(2)由直线
,利用极坐标与直角坐标之间的关系即可得出其直角坐标方程;(2)由直线![]() 经过点
经过点![]() ,可得
,可得![]() 的值,再将直线
的值,再将直线![]() 的参数方程代入曲线
的参数方程代入曲线![]() 的标准方程,由直线参数方程的几何意义可得直线
的标准方程,由直线参数方程的几何意义可得直线![]() 被曲线
被曲线![]() 截得的线段
截得的线段![]() 的长.
的长.
试题解析:(1)由![]() 可得
可得![]() ,即
,即![]() ,
,
∴ 曲线![]() 表示的是焦点为
表示的是焦点为![]() ,准线为
,准线为![]() 的抛物线.
的抛物线.
(2)将![]() 代入
代入![]() ,得
,得![]() ,∴
,∴ ![]() ,
,
∵![]() ,∴
,∴ ![]() ,∴直线
,∴直线![]() 的参数方程为
的参数方程为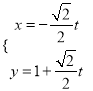 (
(![]() 为参数).
为参数).
将直线![]() 的参数方程代入
的参数方程代入![]() 得
得![]() ,
,
由直线参数方程的几何意义可知,
![]() .
.

练习册系列答案
 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案
相关题目
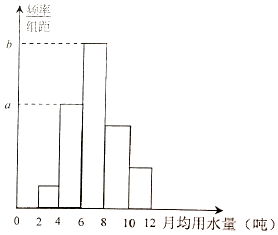
【题目】从某小区随机抽取40个家庭,收集了这40个家庭去年的月均用水量(单位:吨)的数据,整理得到频数分布表和频率分布直方图.
分组 | 频数 |
[2,4) | 2 |
[4,6) | 10 |
[6,8) | 16 |
[8,10) | 8 |
[10,12] | 4 |
合计 | 40 |
(1)求频率分布直方图中a,b的值;
(2)从该小区随机选取一个家庭,试估计这个家庭去年的月均用水量不低于6吨的概率;
(3)在这40个家庭中,用分层抽样的方法从月均用水量不低于6吨的家庭里抽取一个容量为7的样本,将该样本看成一个总体,从中任意选取2个家庭,求其中恰有一个家庭的月均用水量不低于8吨的概率.