题目内容
【题目】已知椭圆C: ![]() =1(a>b>0)的焦距为2
=1(a>b>0)的焦距为2 ![]() ,长轴长为4.
,长轴长为4.
(Ⅰ)求椭圆C的标准方程;
(Ⅱ)如图,过坐标原点O作两条互相垂直的射线,与椭圆C交于A,B两点.设A(x1 , y1),B(x2 , y2),直线AB的方程为y=﹣2x+m(m>0),试求m的值.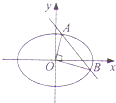
【答案】解:(Ⅰ)∵椭圆C: ![]() =1(a>b>0)的焦距为2
=1(a>b>0)的焦距为2 ![]() ,长轴长为4,
,长轴长为4,
∴c= ![]() ,a=2,
,a=2,
∴b=1,
∴椭圆C的标准方程为 ![]() =1;
=1;
(Ⅱ)直线AB的方程为y=﹣2x+m(m>0),代入椭圆方程得
17x2﹣16mx+4m2﹣4=0,
则x1+x2= ![]() ,x1x2=
,x1x2= ![]() ,①
,①
由OA⊥OB,
知x1x2+y1y2=x1x2+(﹣2x1+m)(﹣2x2+m)
=5x1x2﹣2m(x1+x2)+m2=0,
将①代入,得5× ![]() ﹣2m×
﹣2m× ![]() +m2=0,
+m2=0,
∵m>0,
∴m=2.
【解析】(Ⅰ)利用椭圆C: ![]() =1(a>b>0)的焦距为2
=1(a>b>0)的焦距为2 ![]() ,长轴长为4,求出椭圆的几何量,可得椭圆C的标准方程;(Ⅱ)直线AB、联立椭圆方程,消去y,运用韦达定理,由OA⊥OB,则有x1x2+y1y2=0,化简整理即可求m的值.
,长轴长为4,求出椭圆的几何量,可得椭圆C的标准方程;(Ⅱ)直线AB、联立椭圆方程,消去y,运用韦达定理,由OA⊥OB,则有x1x2+y1y2=0,化简整理即可求m的值.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目