题目内容
【题目】在长方体ABCD﹣A1B1C1D1中，B1 C和C1D与底面A1B1C1D1所成的角分别为60°和45°，则异面直线B1C和C1D所成角的余弦值为（ ）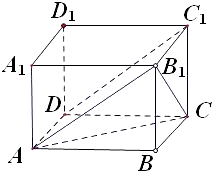 
A.
B.
C.
D.
【答案】A
【解析】解：设长方体的高为1，连接B1A、B1C、AC
∵B1C和C1D与底面所成的角分别为600和450 ，
∴∠B1CB=60°，∠C1DC=45°
∴C1D= 
，B1C= 
，BC= 
，CD=1则AC=
∵C1D∥B1A
∴∠AB1C为异面直线B1C和DC1所成角
由余弦定理可得cos∠AB1C= 
故选A
【考点精析】认真审题，首先需要了解异面直线及其所成的角(异面直线所成角的求法：1、平移法：在异面直线中的一条直线中选择一特殊点，作另一条的平行线；2、补形法：把空间图形补成熟悉的或完整的几何体，如正方体、平行六面体、长方体等，其目的在于容易发现两条异面直线间的关系)．
练习册系列答案
相关题目
【题目】已知某蔬菜商店买进的土豆
（吨）与出售天数
（天）之间的关系如下表所示：
| 2 | 3 | 4 | 5 | 6 | 7 | 9 | 12 |
| 1 | 2 | 3 | 3 | 4 | 5 | 6 | 8 |
（1）请根据上表数据在所给网格纸中绘制散点图；
（2）请根据上表提供的数据，用最小二乘法求出
关于
的线性回归方程
（其中
保留2位有效数字）；
（3）根据（2）中的计算结果，若该蔬菜商店买进土豆40吨，则预计可以销售多少天（计算结果保留整数）？
附： 
， 
