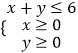Question

【题目】已知f（x）= 是（﹣∞，+∞）上的减函数，那么a的取值范围是

Answer 1

【答案】 ≤a＜
【解析】解：∵当x≥1时，y=logax单调递减，
∴0＜a＜1；
而当x＜1时，f（x）=（3a﹣1）x+4a单调递减，
∴a＜ ；
又函数在其定义域内单调递减，
故当x=1时，（3a﹣1）x+4a≥logax，得a≥ ，
综上可知， ≤a＜ ．
所以答案是： ≤a＜
【考点精析】解答此题的关键在于理解函数单调性的性质的相关知识，掌握函数的单调区间只能是其定义域的子区间 ,不能把单调性相同的区间和在一起写成其并集，以及对对数函数的单调性与特殊点的理解，了解过定点（1，0），即x=1时，y=0;a>1时在（0，+∞）上是增函数;0>a>1时在（0，+∞）上是减函数．