题目内容
如图,已知一四棱锥P-ABCD的底面是边长为1的正方形,且侧棱PC⊥底面ABCD,且PC=2,E是侧棱PC上的动点
(1)求四棱锥P-ABCD的体积;
(2)证明:BD⊥AE。
(3)求二面角P-BD-C的正切值。
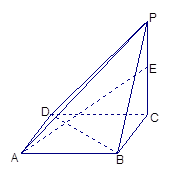
(1)求四棱锥P-ABCD的体积;
(2)证明:BD⊥AE。
(3)求二面角P-BD-C的正切值。

(1) ;(2)见解析;(3)
;(2)见解析;(3) .
.
 ;(2)见解析;(3)
;(2)见解析;(3) .
.试题分析:(1)根据四棱锥P-ABCD的底面是边长为1的正方形,侧棱PC⊥底面ABCD,知高为PC="2." 应用体积计算公式即得;
(2)连结AC,根据ABCD是正方形,得到BD⊥AC ,由PC⊥底面ABCD 得到BD⊥PC,推出BD⊥平面PAC;由于不论点E在何位置,都有AE
 平面PAC,故得BD⊥AE;
平面PAC,故得BD⊥AE;(3)设
 相交于
相交于 ,连
,连 ,可知
,可知 是二面角P-BD-C的的一个平面角,计算其正切即得二面角P-BD-C的正切值.
是二面角P-BD-C的的一个平面角,计算其正切即得二面角P-BD-C的正切值.试题解析:(1)该四棱锥P-ABCD的底面是边长为1的正方形,
侧棱PC⊥底面ABCD,且PC="2."
∴
 4分
4分(2)连结AC,∵ABCD是正方形
∴BD⊥AC ∵PC⊥底面ABCD 且
 平面
平面 ∴BD⊥PC
∴BD⊥PC 又∵
 ∴BD⊥平面PAC
∴BD⊥平面PAC ∵不论点E在何位置,都有AE
 平面PAC
平面PAC ∴BD⊥AE 8分

(3)设
 相交于
相交于 ,连
,连 ,由四棱锥P-ABCD的底面是边长为1的正方形,PC⊥底面ABCD知,
,由四棱锥P-ABCD的底面是边长为1的正方形,PC⊥底面ABCD知, 是二面角P-BD-C的的一个平面角,
是二面角P-BD-C的的一个平面角, ,即二面角P-BD-C的正切值为
,即二面角P-BD-C的正切值为 .
.
练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目


 ,则其外接球的表面积为( ).
,则其外接球的表面积为( ).

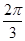 ,那么它的表面积为___________.
,那么它的表面积为___________.




 的长方形ABCD中,以A为圆心画一个扇形,以O为圆心画一个圆,M,N,K为切点,以扇形为圆锥的侧面,以圆O为圆锥底面,围成一个圆锥,求圆锥的全面积与体积.
的长方形ABCD中,以A为圆心画一个扇形,以O为圆心画一个圆,M,N,K为切点,以扇形为圆锥的侧面,以圆O为圆锥底面,围成一个圆锥,求圆锥的全面积与体积.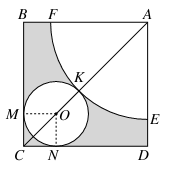
 中,
中, 是边长为4的正三角形,平面
是边长为4的正三角形,平面 平面
平面 ,
, ,
, 为
为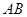 的中点.
的中点.
 ;
; 的余弦值;
的余弦值; 到平面
到平面 的距离.
的距离.