题目内容
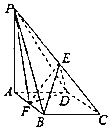
【题目】如图,椭圆![]() 的离心率为
的离心率为![]() ,以椭圆
,以椭圆![]() 的上顶点
的上顶点![]() 为圆心作圆,
为圆心作圆,
![]() ,圆
,圆![]() 与椭圆
与椭圆![]() 在第一象限交于点
在第一象限交于点![]() ,在第二象限交于点
,在第二象限交于点![]() .
.
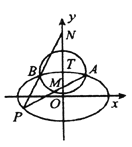
(1)求椭圆![]() 的方程;
的方程;
(2)求![]() 的最小值,并求出此时圆
的最小值,并求出此时圆![]() 的方程;
的方程;
(3)设点![]() 是椭圆
是椭圆![]() 上异于
上异于![]() 的一点,且直线
的一点,且直线![]() 分别与
分别与![]() 轴交于点
轴交于点![]() 为坐标原点,求证:
为坐标原点,求证:
![]() 为定值.
为定值.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)详见解析.
;(3)详见解析.
【解析】试题分析:(1)依据题设条件求出参数即可;(2)依据题设条件及向量的数量积公式建立目标函数,再借助该函数取得最小值时求出圆的方程;(3)借助直线与椭圆的位置关系进行分析推证:
试题解析:
(1) 由题意知, ![]() ,得
,得![]() .
.
故椭圆![]() 的方程为
的方程为![]() .
.
(2) ![]() 点
点![]() 与点
与点![]() 关于
关于![]() 轴对称,设
轴对称,设![]() ,由点
,由点![]() 椭圆
椭圆![]() 上,则
上,则![]() ,得
,得![]()
![]() .由题意知,
.由题意知, ![]() ,
,![]() 当
当![]() 时,
时, ![]() 取得最小值
取得最小值![]() .此时,
.此时, ![]() ,故
,故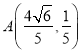 .又点
.又点![]() 在圆
在圆![]() 上,代入圆的方程,得
上,代入圆的方程,得![]() .
.
故圆![]() 的方程为
的方程为![]() .
.
(3)设![]() ,则
,则![]() 的方程为
的方程为![]() .令
.令![]() ,得
,得![]() .同理可得,
.同理可得, ![]() . 故
. 故![]() . ①
. ①
![]() 都在椭圆
都在椭圆![]() 上,
上, ![]() ,代入①得,
,代入①得, 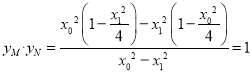 .即得
.即得![]() 为定值.
为定值.

练习册系列答案
 轻松暑假总复习系列答案
轻松暑假总复习系列答案
相关题目