Question

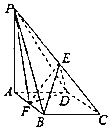
【题目】如图：在四棱锥P﹣ABCD中，底面ABCD是菱形，∠BAD=60°，AB=2，PA=3，PA⊥底面ABCD，E是PC中点，F是AB中点．

（Ⅰ）求证：BE∥平面PDF；

（Ⅱ）求直线PD与平面PFB所成角的正切值；

（Ⅲ）求三棱锥P﹣DEF的体积．

Answer 1

【答案】（Ⅰ）见解析；（Ⅱ） ；（Ⅲ）.

【解析】试题解析：（Ⅰ）利用三角形的中位线定理、平行四边形的判定与性质定理及线面平行的判定定理即可证明取的中点为，连接，则可证四边形是平行四边形，得出，从而证明结论；（Ⅱ）先证⊥， ⊥，利用线面垂直的性质定理可证明⊥平面可得∠为直线与平面所成角，利用直角三角形选择求求其正切值，即可得结果；（Ⅲ）利用等积变形和三棱锥的体积计算公式可得==.

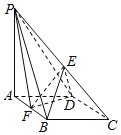
（Ⅰ）证明：取中点，连，;

因为，分别为， 中点，所以， ∥;

且是中点， ， ∥;

且∥，

则四边形为平行四边形

所以∥，且 平面; 平面；

（Ⅱ）解：因为⊥底面， 底面，所以⊥；

又因为底面是菱形， =2， =1，∠=，则,

+ = ， ⊥，

且, 所以⊥平面,

则是在平面内的射影，

∠为直线与平面所成角，

==

（Ⅲ）解：因为是中点，点到平面的距离等于点到平面的距离,

==.

【方法点晴】本题主要考查线面平行的判定定理、直线和平面成的角的定义及求法、利用等积变换求三棱锥体积，属于难题.证明线面平行的常用方法：①利用线面平行的判定定理，使用这个定理的关键是设法在平面内找到一条与已知直线平行的直线，可利用几何体的特征，合理利用中位线定理、线面平行的性质或者构造平行四边形、寻找比例式证明两直线平行.②利用面面平行的性质，即两平面平行，在其中一平面内的直线平行于另一平面. 本题（1）是就是利用方法①证明的.