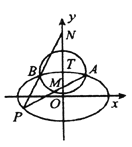
��Ŀ����
����Ŀ���ִ�![]() ��ij�ۿڽ�һЩ��Ʒ�͵������е��ִ�
��ij�ۿڽ�һЩ��Ʒ�͵������е��ִ�![]() �ϣ����ִ�
�ϣ����ִ�![]() ����ʱ���ִ�
����ʱ���ִ�![]() λ�ڸۿ�
λ�ڸۿ�![]() ��ƫ��
��ƫ��![]() ����
����![]() ���20�����
���20�����![]() ����������30����ĺ�������������������ʻ�������ִ�
����������30����ĺ�������������������ʻ�������ִ�![]() ��ֱ�߷�����
��ֱ�߷�����![]() ����/Сʱ�ĺ���������ʻ������
����/Сʱ�ĺ���������ʻ������![]() Сʱ���ִ�
Сʱ���ִ�![]() ����.
����.
��1����ʹ����ʱ�ִ�![]() ������̣����ִ�
������̣����ִ�![]() �ĺ����ٶȴ�СӦΪ���٣�
�ĺ����ٶȴ�СӦΪ���٣�
��2�������ִ�![]() ����ߺ���ֻ�ܴﵽ30����/Сʱ�����ִ�
����ߺ���ֻ�ܴﵽ30����/Сʱ�����ִ�![]() �Զ���ٶȼ�ʲô���з�����������ʱ�����ִ�
�Զ���ٶȼ�ʲô���з�����������ʱ�����ִ�![]() ��������˵������.
��������˵������.
���𰸡���1���ִ�![]() ��
��![]() ����/Сʱ���ٶȺ��У�����ʱ�ִ�
����/Сʱ���ٶȺ��У�����ʱ�ִ�![]() ������̣���2������Ϊ��ƫ��
������̣���2������Ϊ��ƫ��![]() ������Ϊ30����/Сʱ���ִ�
������Ϊ30����/Сʱ���ִ�![]() �������ʱ�����ִ�
�������ʱ�����ִ�![]() ����.
����.
�������������������1�������ִ���![]() ����������
����������![]() �У��������Ҷ����ó�
�У��������Ҷ����ó�![]() ����t�ĺ������Ӷ��ó�
����t�ĺ������Ӷ��ó�![]() ����Сֵ�����Ӧ��
����Сֵ�����Ӧ��![]() ���ó��ٶȣ�
���ó��ٶȣ�
��2���������Ҷ������㺽��ʱ��![]() ���ó�
���ó�![]() ���룬�Ӷ��ó�
���룬�Ӷ��ó�![]() �Ķ������ó����з�����
�Ķ������ó����з�����
�����������1��������ʱ�ִ�![]() ���еľ���Ϊ
���еľ���Ϊ![]() �����
�����
![]()
![]()
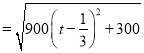 .
.
�൱![]() ʱ��
ʱ�� ![]() ��
�� 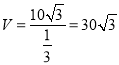 ��
��
���ִ�![]() ��
��![]() ����/Сʱ���ٶȺ��У�����ʱ�ִ�
����/Сʱ���ٶȺ��У�����ʱ�ִ�![]() �������.
�������.
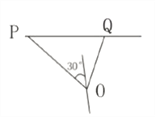
��2�����ִ�![]() ���ִ�
���ִ�![]() ��
��![]() ����������
����������![]()
![]() ��
��
��![]() .
.
��![]() ��
��
��![]() ����
����![]() �����
�����![]() ����
����![]() ʱ
ʱ![]() ��
��
��![]() ʱ��
ʱ�� ![]() ��С��Ϊ
��С��Ϊ![]() ����ʱ
����ʱ![]() ��
��![]() ��
��
�ຽ��Ϊ��ƫ��![]() ������Ϊ30����/Сʱ��
������Ϊ30����/Сʱ��
�ִ�![]() �������ʱ�����ִ�
�������ʱ�����ִ�![]() ����.
����.

����Ŀ��ij�����̴����һˮֳ������һ��С��Ϻ���������ȡ40ֻ����ͳ�ƣ�����������ͳ�ƽ������ͼ��
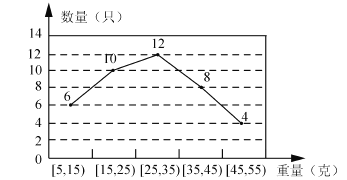
��1�����¼�![]() Ϊ����������С��Ϻ����ȡһֻ������������35
Ϊ����������С��Ϻ����ȡһֻ������������35![]() ��С��Ϻ������
��С��Ϻ������![]() �Ĺ���ֵ��
�Ĺ���ֵ��
��2���Թ�������С��Ϻ��ƽ��������
��3��Ϊ��Ӧ�г������ƶ��������ԣ��þ������ֽ�����С��Ϻ�ֳ������ȼ������ƶ������۵��ۣ����±���
�ȼ� | һ��Ʒ | ����Ʒ | ����Ʒ |
������ |
|
|
|
���ۣ�Ԫ/ֻ�� | 1.2 | 1.5 | 1.8 |
�Թ���þ�������ÿǧ���������Ԫ��ȡ�������չ�����С��Ϻ�����ܻ������