题目内容
【题目】已知![]() ,
, ![]() 分别是椭圆
分别是椭圆![]() :
: ![]() (
(![]() )的左、右焦点,离心率为
)的左、右焦点,离心率为![]() ,
, ![]() ,
, ![]() 分别是椭圆的上、下顶点,
分别是椭圆的上、下顶点, ![]() .
.
(1)求椭圆![]() 的方程;
的方程;
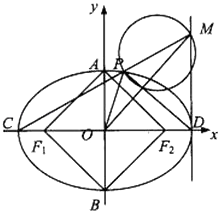
(2)过![]() 作直线
作直线![]() 与
与![]() 交于
交于![]() ,
, ![]() 两点,求三角形
两点,求三角形![]() 面积的最大值(
面积的最大值(![]() 是坐标原点).
是坐标原点).
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】试题分析:(1)根据离心率为![]() ,
, ![]() ,列出关于
,列出关于![]() 、
、![]() 、
、![]() 的方程组,结合性质
的方程组,结合性质![]() ,求出
,求出![]() 、
、![]() 、
、![]() ,即可得椭圆
,即可得椭圆![]() 的方程;(2)直线
的方程;(2)直线![]() 斜率存在,设其方程为
斜率存在,设其方程为![]() .,直线方程与椭圆方程联立,根据韦达定理,弦长公式、点到直线距离公式及三角形面积公式将角形
.,直线方程与椭圆方程联立,根据韦达定理,弦长公式、点到直线距离公式及三角形面积公式将角形![]() 面积用
面积用![]() 表示,利用基本不等式 即可得结果.
表示,利用基本不等式 即可得结果.
试题解析:(1)由题知, ![]() ,
, ![]() ,
, ![]() ,
,
∴![]() ,∴
,∴![]() ,①
,①
∵![]() ,∴
,∴![]() ,∴
,∴![]() ,②
,②
①②联立解得![]() ,
, ![]() ,∴椭圆
,∴椭圆![]() 的方程为
的方程为![]() .
.
(2)设![]() ,
, ![]() ,显然直线
,显然直线![]() 斜率存在,设其方程为
斜率存在,设其方程为![]() ,
,
代入![]() ,整理得
,整理得![]() ,
,
则![]() ,即
,即![]() ,
, ![]() ,
, ![]() ,
,
![]()
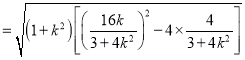
 ,
,
所以![]() 到
到![]() 的距离
的距离![]() ,
,
所以三角形![]() 面积
面积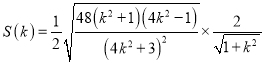
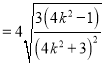 ,
,
设![]() ,所以
,所以 ,
,
当且仅当![]() ,即
,即![]() ,即
,即![]() ,即
,即![]() 时取等号,
时取等号,
所以![]() 面积的最大值为
面积的最大值为![]() .
.
【方法点晴】本题主要考查待定系数法求椭圆方程及圆锥曲线求最值,属于难题.解决圆锥曲线中的最值问题一般有两种方法:一是几何意义,特别是用圆锥曲线的定义和平面几何的有关结论来解决,非常巧妙;二是将圆锥曲线中最值问题转化为函数问题,然后根据函数的特征选用参数法、配方法、判别式法、三角函数有界法、函数单调性法以及均值不等式法,本题(2)就是用的这种思路,利用均值不等式法求三角形最值的.

练习册系列答案
 小题狂做系列答案
小题狂做系列答案
相关题目
【题目】对某电子元件进行寿命追踪调查,情况如下.
寿命(h) | 100~200 | 200~300 | 300~400 | 400~500 | 500~600 |
个 数 | 20 | 30 | 80 | 40 | 30 |
(1)列出频率分布表;
(2)画出频率分布直方图;
(3)估计元件寿命在100~400h以内的在总体中占的比例.