题目内容
【题目】已知椭圆 
的左、右焦点分别为F1、F2 ， 短轴两个端点为A、B，且四边形F1AF2B是边长为2的正方形． 
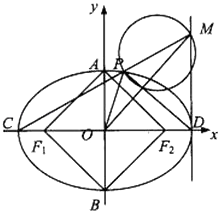
（1）求椭圆的方程；
（2）若C、D分别是椭圆长的左、右端点，动点M满足MD⊥CD，连接CM，交椭圆于点P．证明： 
为定值．
（3）在（2）的条件下，试问x轴上是否存异于点C的定点Q，使得以MP为直径的圆恒过直线DP、MQ的交点，若存在，求出点Q的坐标；若不存在，请说明理由．
【答案】
（1）解：a=2，b=c，a2=b2+c2，∴b2=2；
∴椭圆方程为 
（2）解：C（﹣2，0），D（2，0），设M（2，y0），P（x1，y1），
则 
直线CM： 
，代入椭圆方程x2+2y2=4，
得 
∵x1=﹣ 
，∴ 
，∴ 
，∴ 
∴ 
（定值）
（3）解：设存在Q（m，0）满足条件，则MQ⊥DP
则由 
，从而得m=0
∴存在Q（0，0）满足条件
【解析】（1）由题意知a=2，b=c，b2=2，由此可知椭圆方程为 ．（2）设M（2，y0），P（x1 ， y1），则 ，直线CM： ，代入椭圆方程x2+2y2=4，得 ，然后利用根与系数的关系能够推导出 
为定值．（3）设存在Q（m，0）满足条件，则MQ⊥DP． ，再由 ，由此可知存在Q（0，0）满足条件．
【考点精析】利用椭圆的标准方程对题目进行判断即可得到答案，需要熟知椭圆标准方程焦点在x轴：
，焦点在y轴：
．
练习册系列答案
相关题目
