题目内容
【题目】已知椭圆![]() 的短轴长为
的短轴长为![]() ,左右焦点分别为
,左右焦点分别为![]() ,
,![]() ,点
,点![]() 是椭圆上位于第一象限的任一点,且当
是椭圆上位于第一象限的任一点,且当![]() 时,
时,![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)若椭圆![]() 上点
上点![]() 与点
与点![]() 关于原点
关于原点![]() 对称,过点
对称,过点![]() 作
作![]() 垂直于
垂直于![]() 轴,垂足为
轴,垂足为![]() ,连接
,连接![]() 并延长交
并延长交![]() 于另一点
于另一点![]() ,交
,交![]() 轴于点
轴于点![]() .
.
(ⅰ)求![]() 面积最大值;
面积最大值;
(ⅱ)证明:直线![]() 与
与![]() 斜率之积为定值.
斜率之积为定值.
【答案】(1)![]() ;(2)(ⅰ)
;(2)(ⅰ)![]() ;(ⅱ)证明见解析.
;(ⅱ)证明见解析.
【解析】
(1)由![]() ,
,![]() 解方程组即可得到答案;
解方程组即可得到答案;
(2)(ⅰ)设![]() ,
,![]() ,则
,则![]() ,
,![]() ,易得
,易得![]() ,注意到
,注意到![]() ,利用基本不等式得到
,利用基本不等式得到![]() 的最大值即可得到答案;(ⅱ)设直线
的最大值即可得到答案;(ⅱ)设直线![]() 斜率为
斜率为![]() ,直线
,直线![]() 方程为
方程为![]() ,联立椭圆方程得到
,联立椭圆方程得到![]() 的坐标,再利用两点的斜率公式计算即可.
的坐标,再利用两点的斜率公式计算即可.
(1)设![]() ,由
,由![]() ,得
,得![]() .
.
将![]() 代入
代入![]() ,得
,得![]() ,即
,即![]() ,
,
由![]() ,解得
,解得![]() ,
,
所以椭圆![]() 的标准方程为
的标准方程为![]() .
.
(2)设![]() ,
,![]() ,则
,则![]() ,
,![]()
(ⅰ)易知![]() 为
为![]() 的中位线,所以
的中位线,所以![]() ,
,
所以![]() ,
,
又![]() 满足
满足![]() ,所以
,所以
![]() ,得
,得![]() ,
,
故![]() ,当且仅当
,当且仅当![]() ,即
,即![]() ,
,![]() 时取等号,
时取等号,
所以![]() 面积最大值为
面积最大值为![]() .
.
(ⅱ)记直线![]() 斜率为
斜率为![]() ,则直线
,则直线![]() 斜率为
斜率为![]() ,
,
所以直线![]() 方程为
方程为![]() .
.
由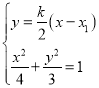 ,得
,得![]() ,
,
由韦达定理得![]() ,所以
,所以![]() ,
,
代入直线![]() 方程,得
方程,得![]() ,
,
于是,直线![]() 斜率
斜率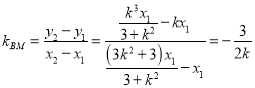 ,
,
所以直线![]() 与
与![]() 斜率之积为定值
斜率之积为定值![]() .
.

练习册系列答案
相关题目
【题目】某校为了解家长对学校食堂的满意情况,分别从高一、高二年级随机抽取了20位家长的满意度评分,其频数分布表如下:
满意度评分分组 |
|
|
|
|
| 合计 |
高一 | 1 | 3 | 6 | 6 | 4 | 20 |
高二 | 2 | 6 | 5 | 5 | 2 | 20 |
根据评分,将家长的满意度从低到高分为三个等级:
满意度评分 | 评分 | 70 | 评分 |
满意度等级 | 不满意 | 满意 | 非常满意 |
假设两个年级家长的评价结果相互独立,根据所给数据,以事件发生的频率作为相应事件发生的概率.现从高一、高二年级各随机抽取1名家长,记事件![]() :“高一家长的满意度等级高于高二家长的满意度等级”,则事件
:“高一家长的满意度等级高于高二家长的满意度等级”,则事件![]() 发生的概率为__________.
发生的概率为__________.