题目内容
【题目】如图，在平面直角坐标系xOy中，已知R（x0 ， y0）是椭圆 
+ 
=1上的一点，从原点O向圆R（x﹣x0）2+（y﹣y0）2=12作两条切线，分别交椭圆于P，Q两点． 
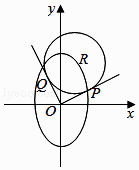
（1）若R点在第一象限，且直线OP，OQ互相垂直，求圆R的方程；
（2）若直线OP，OQ的斜率存在，分别记为k1 ， k2 ， 求k1k2的值．
【答案】
（1）解：圆R的半径r=2 
，
∵OP⊥OQ，∴|OR|= 
r=2 
，∴x02+y02=24，
又点R在椭圆C上，∴ 
，
联立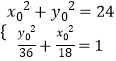 
，解得 
．
∴圆R的方程为 （x﹣2 ）2+（y﹣2 ）2=12
（2）解：直线OP方程为：k1x﹣y=0，直线OQ的方程为：k2x﹣y=0．
∵OP，OQ为圆R的切线，
∴ 
=2 ， 
．
∴k1，k2为方程 
的两根，
∴ 
，
∵点R在椭圆C上，∴ ，即 
，
∴ 
．
【解析】（1）利用切线的性质可求出|OR|=2 ，又R在椭圆上．列方程组解出R点坐标；（2）根据R到OP，OQ的距离为2 得出k1 ， k2为某个一元二次方程的解，根据距离公式得出这个一元二次方程，结合R为椭圆上的点得出k1k2的值．
练习册系列答案
相关题目
