��Ŀ����
����Ŀ��ijӪ��ѧ�ҽ��飺������ÿ��ĵ�����������������[60��90]����λ���ˣ���֬����������������[18��27]����λ���ˣ���ijѧУʳ���ṩ�Ļ�ʳ��ʳ��A��ʳ��BΪ����1ǧ��ʳ��A��������60�ˣ���֬��9�ˣ��ۼ�20Ԫ��1ǧ��ʳ��B��������30�ˣ���֬��27�ˣ��ۼ�15Ԫ�� �������ijѧ��ֻ��ʳ��A���ж����Ļ�ʳ�Ƿ����Ӫ��ѧ�ҵĽ��飬��˵�����ɣ�
����Ϊ�˻�������ҷ���Ӫ��ѧ�ҵĽ��飬ѧ����Ҫÿ��ͬʱʳ��ʳ��A��ʳ��B������ǧ�ˣ�����������Ҫ���ѵ�Ǯ����
���𰸡��⣺�������ѧ��ֻ��ʳ��Axkg�� �� ![]() ��
��
�⣬
�ʲ�����Ӫ��ѧ�ҵĽ��飻
���������⣬��ѧ��ÿ���ʳ��Axkg��ʳ��Bykg��
��z=20x+15y��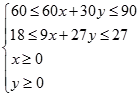
��ƽ���������£�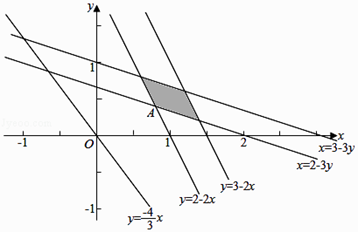 ��
��
�� ![]() ��ã�x=
��ã�x= ![]() ��y=
��y= ![]() ��
��
��z=20�� ![]() +15��
+15�� ![]() =22��
=22��
��ѧ��ÿ���0.8ǧ��ʳ��A��0.4ǧ��ʳ��B�����ܷ���Ӫ��ѧ�ҵĽ����ֻ������٣�
�����Ҫ����22Ԫ
���������������ѧ��ֻ��ʳ��Axkg���Ӷ��ò���ʽ�� ![]() ���Ƿ��н⼴�ɣ����������⣬��ѧ��ÿ���ʳ��Axkg��ʳ��Bykg���Ӷ��õ�Ŀ�꺯��z=20x+15y������Լ������
���Ƿ��н⼴�ɣ����������⣬��ѧ��ÿ���ʳ��Axkg��ʳ��Bykg���Ӷ��õ�Ŀ�꺯��z=20x+15y������Լ������ 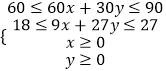 ���Ӷ��������Թ滮��⼴�ɣ�
���Ӷ��������Թ滮��⼴�ɣ�

��ϰ��ϵ�д�
�����Ŀ