题目内容
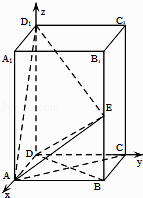
【题目】在长方体ABCD﹣A1B1C1D1中,AB=BC=1,AA1=2,E为BB1中点. (Ⅰ)证明:AC⊥D1E;
(Ⅱ)求DE与平面AD1E所成角的正弦值;
(Ⅲ)在棱AD上是否存在一点P,使得BP∥平面AD1E?若存在,求DP的长;若不存在,说明理由.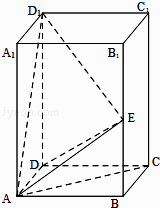
【答案】(Ⅰ)证明:连接BD ∵ABCD﹣A1B1C1D1是长方体,∴D1D⊥平面ABCD,
又AC平面ABCD,∴D1D⊥AC
在长方形ABCD中,AB=BC,∴BD⊥AC
又BD∩D1D=D,∴AC⊥平面BB1D1D,
而D1E平面BB1D1D,∴AC⊥D1E
(Ⅱ)解:如图建立空间直角坐标系Dxyz,则A(1,0,0),D1(0,0,2),E(1,1,1),B(1,1,0),
∴ ![]()
设平面AD1E的法向量为 ![]() ,则
,则 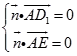 ,即
,即 ![]()
令z=1,则 ![]()
∴ 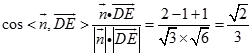
∴DE与平面AD1E所成角的正弦值为 ![]()
(Ⅲ)解:假设在棱AD上存在一点P,使得BP∥平面AD1E.
设P的坐标为(t,0,0)(0≤t≤1),则 ![]()
∵BP∥平面AD1E
∴ ![]() ,即
,即 ![]() ,
,
∴2(t﹣1)+1=0,解得 ![]() ,
,
∴在棱AD上存在一点P,使得BP∥平面AD1E,此时DP的长 ![]() ..
..
【解析】(I)利用线面垂直的判定定理,证明AC⊥平面BB1D1D,即可得到AC⊥D1E;(Ⅱ)建立空间直角坐标系,确定面AD1E的法向量,利用向量的夹角公式,即可求DE与平面AD1E所成角的正弦值;(Ⅲ)利用BP∥平面AD1E,可得 ![]() ,利用向量的数量积公式,可得结论.
,利用向量的数量积公式,可得结论.
【考点精析】通过灵活运用直线与平面平行的判定和直线与平面垂直的性质,掌握平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行;简记为:线线平行,则线面平行;垂直于同一个平面的两条直线平行即可以解答此题.

练习册系列答案
相关题目