题目内容
((本小题满分12分)
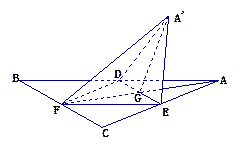
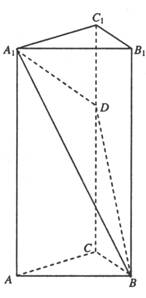
如图,已知在直四棱柱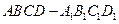 中,
中,
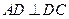 ,
,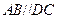 ,
,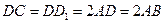
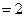 .
.
(1)求证: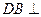 平面
平面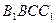 ;
;
(2)求二面角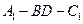 的余弦值.
的余弦值.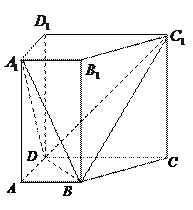
如图,已知在直四棱柱
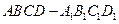 中,
中,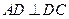 ,
,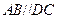 ,
,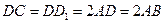
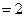 .
.(1)求证:
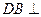 平面
平面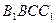 ;
;(2)求二面角
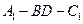 的余弦值.
的余弦值.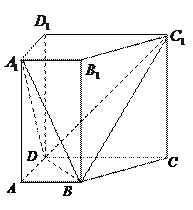
解法一:
(1)设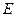 是
是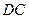 的中点,连结
的中点,连结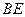 ,则四边形
,则四边形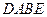 为正方形,
为正方形,
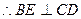 .故
.故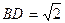 ,
,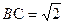 ,
,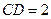 ,
,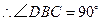 ,即
,即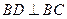 .
.
又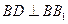 ,
,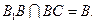
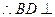 平面
平面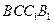 ,…………6分
,…………6分
(2)由(I)知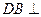 平面
平面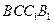 ,
,
又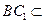 平面
平面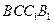 ,
,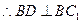 ,
,
取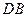 的中点
的中点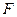 , 连结
, 连结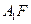 ,又
,又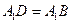 ,则
,则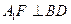 .
.
取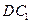 的中点
的中点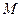 ,连结
,连结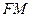 ,则
,则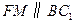 ,
,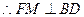 .
.
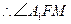 为二面角
为二面角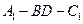 的平面角.
的平面角.
连结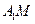 ,在
,在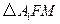 中,
中,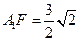 ,
,
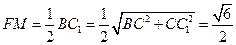 ,
,
取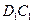 的中点
的中点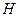 ,连结
,连结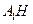 ,
,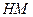 ,
,
在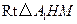 中,
中,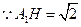 ,
,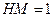 ,
,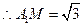 .
.
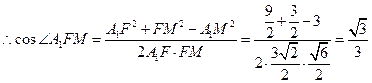 .
.
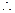 二面角
二面角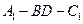 的余弦值为
的余弦值为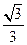 .…………………………12分
.…………………………12分
解法二:
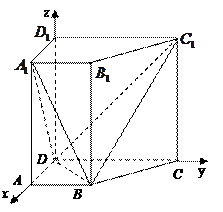 (1)以
(1)以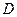 为原点,
为原点,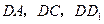 所在直线分别为
所在直线分别为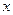 轴,
轴,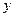 轴,
轴,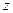 轴建立如图所示的空间直角坐标系,则
轴建立如图所示的空间直角坐标系,则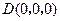 ,
,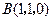 ,
,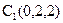 ,
,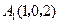 ,
,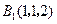 ,
,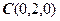 .
.
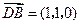 ,
,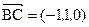 ,
,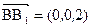
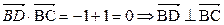
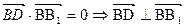
又因为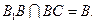 所以,
所以,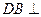 平
平 面
面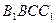 .…6分
.…6分
(2)设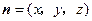 为平面
为平面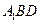 的一个法向量.
的一个法向量.
由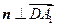
 ,
,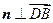 ,
,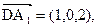
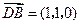
得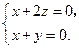 取
取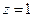 ,则
,则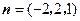 .
.
又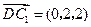 ,
,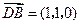 ,设
,设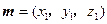 为平面
为平面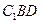 的一个法向量,
的一个法向量,
由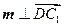 ,
,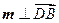 ,得
,得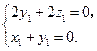 取
取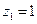 ,则
,则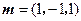 ,
,
设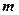 与
与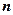 的夹角为
的夹角为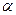 ,二面角
,二面角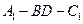 为
为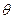 ,显然
,显然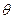 为锐角,
为锐角,
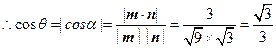 .…………12分
.…………12分
(1)设
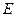 是
是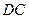 的中点,连结
的中点,连结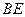 ,则四边形
,则四边形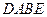 为正方形,
为正方形,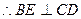 .故
.故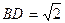 ,
,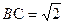 ,
,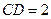 ,
,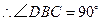 ,即
,即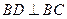 .
.又
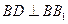 ,
,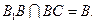
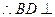 平面
平面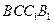 ,…………6分
,…………6分(2)由(I)知
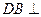 平面
平面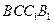 ,
,
又
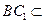 平面
平面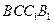 ,
,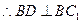 ,
,取
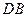 的中点
的中点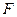 , 连结
, 连结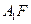 ,又
,又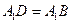 ,则
,则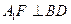 .
.取
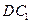 的中点
的中点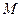 ,连结
,连结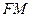 ,则
,则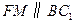 ,
,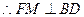 .
.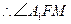 为二面角
为二面角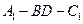 的平面角.
的平面角.连结
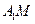 ,在
,在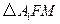 中,
中,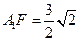 ,
,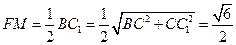 ,
,取
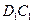 的中点
的中点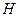 ,连结
,连结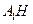 ,
,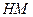 ,
,在
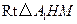 中,
中,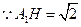 ,
,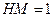 ,
,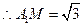 .
.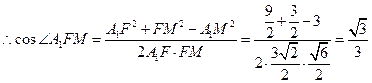 .
.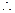 二面角
二面角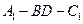 的余弦值为
的余弦值为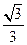 .…………………………12分
.…………………………12分解法二:
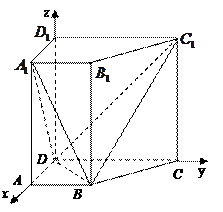 (1)以
(1)以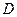 为原点,
为原点,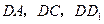 所在直线分别为
所在直线分别为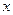 轴,
轴,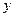 轴,
轴,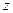 轴建立如图所示的空间直角坐标系,则
轴建立如图所示的空间直角坐标系,则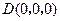 ,
,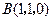 ,
,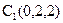 ,
,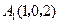 ,
,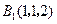 ,
,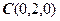 .
.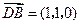 ,
,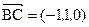 ,
,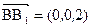
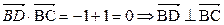
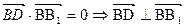
又因为
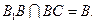 所以,
所以,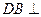 平
平 面
面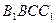 .…6分
.…6分(2)设
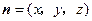 为平面
为平面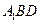 的一个法向量.
的一个法向量.由
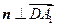
 ,
,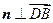 ,
,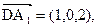
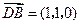
得
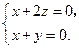 取
取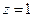 ,则
,则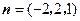 .
.又
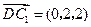 ,
,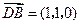 ,设
,设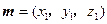 为平面
为平面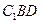 的一个法向量,
的一个法向量,由
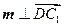 ,
,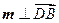 ,得
,得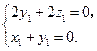 取
取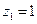 ,则
,则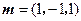 ,
,设
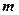 与
与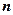 的夹角为
的夹角为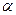 ,二面角
,二面角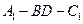 为
为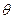 ,显然
,显然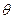 为锐角,
为锐角,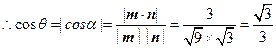 .…………12分
.…………12分略

练习册系列答案
 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案
相关题目

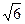 ,∠APB=∠ADB=60°
,∠APB=∠ADB=60°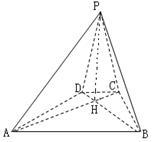
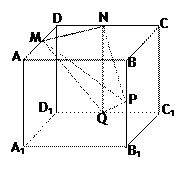
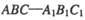 中,AC=BC=1, AAi="3"
中,AC=BC=1, AAi="3"  D为CCi上的点,二面角A-A1B-D的余弦值为
D为CCi上的点,二面角A-A1B-D的余弦值为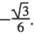
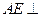 平面CDE
平面CDE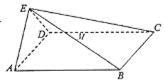
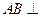 平面ADE;
平面ADE;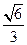 ,试确定点M的位置。
,试确定点M的位置。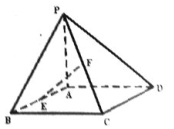
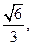 求直线ED与平面PCD所成的角
求直线ED与平面PCD所成的角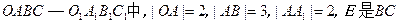 的中点。
的中点。 (1)求直线
(1)求直线
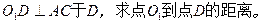
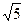 的等腰三角形,则二面角V―AB―C的度数是 。
的等腰三角形,则二面角V―AB―C的度数是 。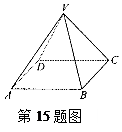
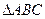 的中线
的中线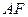 与中位线
与中位线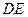 相交
相交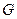 ,
,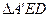 是
是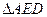 绕
绕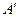 不与
不与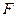 重合).现给出下列四个命题:
重合).现给出下列四个命题: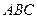 上的射影在线段
上的射影在线段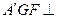 平面
平面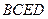 ;
; 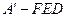 的体积有最大值;
的体积有最大值;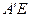 与
与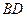 不可能垂直.其中正确的命题的序号是_________.
不可能垂直.其中正确的命题的序号是_________.