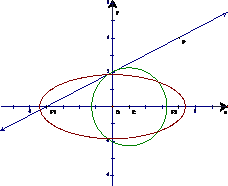
题目内容
已知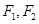 为椭圆E的两个左右焦点,抛物线C以
为椭圆E的两个左右焦点,抛物线C以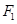 为顶点,
为顶点,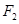 为焦点,设P为椭圆与抛物线的一个交点,如果椭圆离心率e满足
为焦点,设P为椭圆与抛物线的一个交点,如果椭圆离心率e满足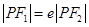 ,则e的值为( )
,则e的值为( )
A. 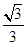 B.
B.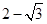 C.
C. 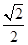 D.
D.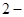
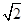
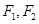 为椭圆E的两个左右焦点,抛物线C以
为椭圆E的两个左右焦点,抛物线C以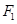 为顶点,
为顶点,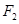 为焦点,设P为椭圆与抛物线的一个交点,如果椭圆离心率e满足
为焦点,设P为椭圆与抛物线的一个交点,如果椭圆离心率e满足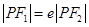 ,则e的值为( )
,则e的值为( )
|
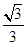 B.
B.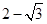 C.
C. 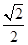 D.
D.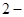
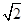
A
根据抛物线定义可知|PF1|=e|PF2|=e(到抛物线准线的距离)推断出抛物线的准线与椭圆的准线重合,进而分别表示出抛物线和椭圆的准线方程,使其相等求得a和c的关系,则椭圆的离心率可得.
解:由椭圆第二定义是|PF1|=e(x+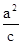 )
)
由抛物线的定义可知到焦点与准线的距离相等|PF1|=e|PF2|=e(到抛物线准线的距离)
∴抛物线的准线与椭圆的准线重合,依题意可知抛物线的准线方程为x=-3c
椭圆准线为x=--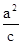
∴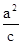 =3c,即a2=3c2,
=3c,即a2=3c2,
∴e=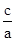 =
=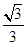
故选A
主要考查了椭圆的应用.解题的关键是判断出椭圆和抛物线的准线重合.
解:由椭圆第二定义是|PF1|=e(x+
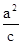 )
)由抛物线的定义可知到焦点与准线的距离相等|PF1|=e|PF2|=e(到抛物线准线的距离)
∴抛物线的准线与椭圆的准线重合,依题意可知抛物线的准线方程为x=-3c
椭圆准线为x=--
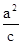
∴
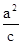 =3c,即a2=3c2,
=3c,即a2=3c2,∴e=
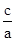 =
=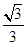
故选A
主要考查了椭圆的应用.解题的关键是判断出椭圆和抛物线的准线重合.

练习册系列答案
 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案
相关题目
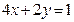 ;②
;②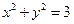 ;③
;③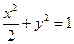 ;④
;④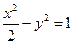 。其中与直线
。其中与直线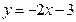 有交点的所有曲线是( )
有交点的所有曲线是( )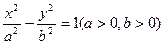 的两焦点,以线段F1F2为边作正三角形MF1F2,若边MF1的中点在双曲线上,则双曲线的离心率是 ( )
的两焦点,以线段F1F2为边作正三角形MF1F2,若边MF1的中点在双曲线上,则双曲线的离心率是 ( )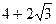
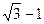

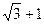
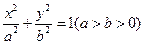 的左准线为l,左右焦点分别为F1、F2,抛物线C2的准线为l,一个焦点为F2,C1与C2的一个交点为P,则
的左准线为l,左右焦点分别为F1、F2,抛物线C2的准线为l,一个焦点为F2,C1与C2的一个交点为P,则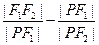 等于( )
等于( )
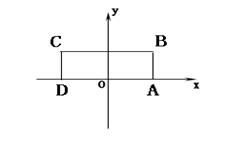
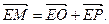 (Ⅰ)求点M的轨迹方程;
(Ⅰ)求点M的轨迹方程;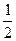 ),过点F的直线l与点M的轨迹相交于Q、R两点,且
),过点F的直线l与点M的轨迹相交于Q、R两点,且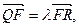 求实数
求实数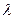 的取值范围.
的取值范围.