题目内容
6.已知数列{an}的前n项和Sn=2an-2n+1+2(n为正整数).(1)证明:数列{$\frac{{a}_{n}}{{2}^{n}}$}是等差数列,并求{an}的通项公式;
(2)令bn=log2a1+log2$\frac{{a}_{2}}{2}$+…+log2$\frac{{a}_{n}}{n}$,设数列{$\frac{1}{{b}_{n}}$}的前n项和为Tn,是否存在实数M,使得Tn≤M对一切正整数都成立?若存在,求出M的最小值;若不存在,请说明理由.
分析 (1)当n=1时,S1=2a1-22+2,当n≥2时,an=Sn-Sn-1=2an-2n+1+2-(2an-1-2n+2)从而可得$\frac{{a}_{n}}{{2}^{n}}$-$\frac{{a}_{n-1}}{{2}^{n-1}}$=1;$\frac{{a}_{1}}{{2}^{1}}$=1;从而证明;再求{an}的通项公式;
(2)化简bn=log2a1+log2$\frac{{a}_{2}}{2}$+…+log2$\frac{{a}_{n}}{n}$=$\frac{(n+1)n}{2}$,从而可得$\frac{1}{{b}_{n}}$=$\frac{2}{(n+1)n}$=2($\frac{1}{n}$-$\frac{1}{n+1}$);利用裂项求和法得Tn=2(1-$\frac{1}{n+1}$)=$\frac{2n}{n+1}$;从而化为$\frac{2n}{n+1}$≤M对一切正整数n都成立;从而解得.
解答 解:(1)证明:①当n=1时,S1=2a1-22+2,
解得,a1=2;
②当n≥2时,an=Sn-Sn-1
=2an-2n+1+2-(2an-1-2n+2)
即an-2an-1-2n=0,
即$\frac{{a}_{n}}{{2}^{n}}$-$\frac{{a}_{n-1}}{{2}^{n-1}}$=1;$\frac{{a}_{1}}{{2}^{1}}$=1;
∴{$\frac{{a}_{n}}{{2}^{n}}$}是以1为首项,1为公差的等差数列;
即$\frac{{a}_{n}}{{2}^{n}}$=n,故an=n×2n.
(2)bn=log2a1+log2$\frac{{a}_{2}}{2}$+…+log2$\frac{{a}_{n}}{n}$
=1+2+3+…+n=$\frac{(n+1)n}{2}$,
$\frac{1}{{b}_{n}}$=$\frac{2}{(n+1)n}$=2($\frac{1}{n}$-$\frac{1}{n+1}$);
Tn=2(1-$\frac{1}{2}$)+2($\frac{1}{2}$-$\frac{1}{3}$)+…+2($\frac{1}{n}$-$\frac{1}{n+1}$)
=2(1-$\frac{1}{n+1}$)=$\frac{2n}{n+1}$;
故$\frac{2n}{n+1}$≤M对一切正整数n都成立;
故M≥2;
故M的最小值为2.
点评 本题考查了等差数列的判断与证明,同时考查了裂项求和法的应用,属于中档题.

| A. | 1、0.、0.8 | B. | 0.6、0.8、1 | C. | 0.6、1、0.8 | D. | 0.6、0.6、0.8 |
| A. | φ:$\left\{\begin{array}{l}{x′=5x}\\{{y}^{′}=4y}\end{array}\right.$ | B. | φ:$\left\{\begin{array}{l}{{x}^{′}=4x}\\{{y}^{′}=5y}\end{array}\right.$ | ||
| C. | φ:$\left\{\begin{array}{l}{{x}^{′}=\frac{1}{4}x}\\{{y}^{′}=\frac{1}{5}y}\end{array}\right.$ | D. | φ:$\left\{\begin{array}{l}{{x}^{′}=\frac{1}{5}x}\\{{y}^{′}=\frac{1}{4}y}\end{array}\right.$ |
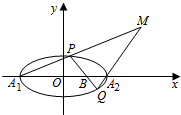 如图,已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的右准线l的方程为x=$\frac{4\sqrt{3}}{3}$,焦距为2$\sqrt{3}$.
如图,已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的右准线l的方程为x=$\frac{4\sqrt{3}}{3}$,焦距为2$\sqrt{3}$.