题目内容
8.若以A、B为焦点的双曲线经过点C,且|AB|=|AC|,cos∠ABC=$\frac{1}{3}$,则该双曲线的离心率为( )| A. | $\frac{3}{2}$ | B. | 2 | C. | 3 | D. | $\frac{5}{2}$ |
分析 先确定C在双曲线的右支上,由双曲线定义知$|{BD}|=\frac{1}{2}|{BC}|=\frac{1}{2}(2c-2a)=c-a$,利用$cos∠ABD=\frac{1}{3}$,可得$\frac{c-a}{2c}=\frac{1}{3}$,即可求出双曲线的离心率.
解答 解:不妨设A、B为左、右焦点,实半轴长为a,半焦距为c,若点C在双曲线的左支上,设BC中点为D,则
由定义知|BD|=$\frac{1}{2}$|BC|=$\frac{1}{2}$(2c+2a)=c+a,
在Rt△ABD中,由cos∠ABC=$\frac{1}{3}$,故$\frac{c+a}{2c}=\frac{1}{3},e=-3$,不可能.
故C在双曲线的右支上,
设BC中点为D,则由双曲线定义知$|{BD}|=\frac{1}{2}|{BC}|=\frac{1}{2}(2c-2a)=c-a$,
在Rt△ABD中,$cos∠ABD=\frac{1}{3}$,故$\frac{c-a}{2c}=\frac{1}{3}$,得$e=\frac{c}{a}=3$.
故选:C.
点评 本题考查双曲线的离心率,考查学生分析解决问题的能力,确定C在双曲线的右支上是关键.

练习册系列答案
相关题目
19.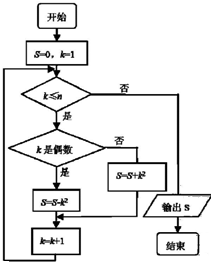 阅读如图所示的程序框图,运行相应的程序,若输入n的值为100,则输出S的值为( )
阅读如图所示的程序框图,运行相应的程序,若输入n的值为100,则输出S的值为( )
 阅读如图所示的程序框图,运行相应的程序,若输入n的值为100,则输出S的值为( )
阅读如图所示的程序框图,运行相应的程序,若输入n的值为100,则输出S的值为( )| A. | -1050 | B. | 5050 | C. | -5050 | D. | -4950 |
16.已知F1是双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的左焦点,过F1且垂直于x轴的直线与双曲线交于A、B两点,E是双曲线的右顶点,若△ABE是钝角三角形,则该双曲线的离心率的取值范围是( )
| A. | (1,$\sqrt{3}$) | B. | ($\sqrt{3}$,2) | C. | (2,+∞) | D. | (1,2) |
13.已知f(x+1)是周期为2的奇函数,当-1≤x≤0时,f(x)=-2x(x+1),则f(-$\frac{3}{2}$)的值为( )
| A. | $\frac{1}{2}$ | B. | $\frac{1}{4}$ | C. | -$\frac{1}{4}$ | D. | -$\frac{1}{2}$ |
 如图,圆O中AB=4为直径,直线CE与圆O相切于点C,AD⊥CE于点D,若AD=1,∠ACD=θ,则cosθ=$\frac{\sqrt{3}}{2}$.
如图,圆O中AB=4为直径,直线CE与圆O相切于点C,AD⊥CE于点D,若AD=1,∠ACD=θ,则cosθ=$\frac{\sqrt{3}}{2}$.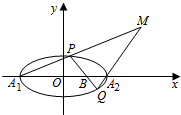 如图,已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的右准线l的方程为x=$\frac{4\sqrt{3}}{3}$,焦距为2$\sqrt{3}$.
如图,已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的右准线l的方程为x=$\frac{4\sqrt{3}}{3}$,焦距为2$\sqrt{3}$.