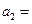题目内容
(12分)设数列{an},{bn}都是等差数列,它们的前n项的和分别为Sn , Tn,若对一切n ∈ N*,都有Sn+3 = Tn.(1)若a1 ≠ b1,试分别写出一个符号条件的数列{an}和{bn};(2)若a1 + b1 = 1,数列{cn}满足:cn = 4 an + l(–1)n–12bn,且当n ∈ N*时,cn+1 ≥ cn恒成立,求实数l的最大值.
(2)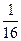
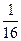
(1)答案不唯一,例如 ,
,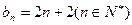
(2)设数列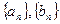 的公差分别是
的公差分别是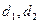 ,
,
则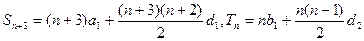
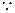 对一切
对一切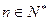 ,有
,有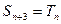 ,
, 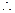
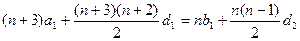
即: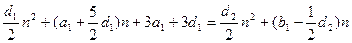
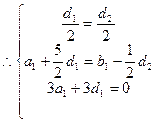 即
即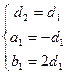
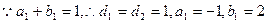
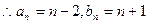
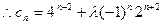
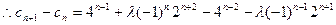
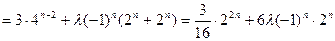
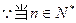 时,
时,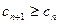 恒成立,即
恒成立,即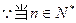 时,
时,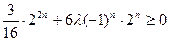 恒成立
恒成立
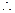 当
当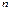 为正奇数时,
为正奇数时,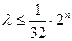 恒成立,而
恒成立,而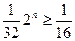 ,
,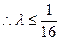 ;
;
当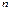 为正偶数时,
为正偶数时,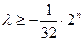 恒成立,而
恒成立,而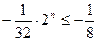 ,
,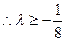
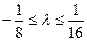
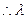 的最大值是
的最大值是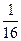 .
.
 ,
,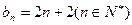
(2)设数列
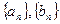 的公差分别是
的公差分别是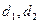 ,
,则
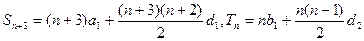
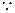 对一切
对一切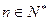 ,有
,有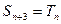 ,
, 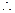
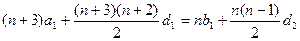
即:
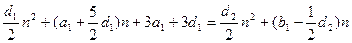
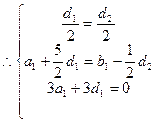 即
即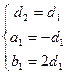
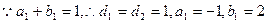
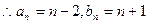
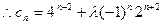
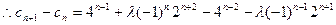
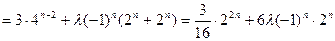
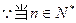 时,
时,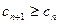 恒成立,即
恒成立,即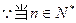 时,
时,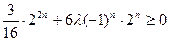 恒成立
恒成立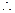 当
当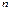 为正奇数时,
为正奇数时,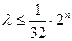 恒成立,而
恒成立,而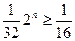 ,
,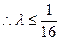 ;
;当
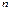 为正偶数时,
为正偶数时,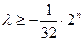 恒成立,而
恒成立,而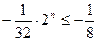 ,
,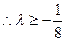
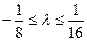
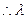 的最大值是
的最大值是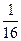 .
.
练习册系列答案
相关题目
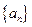 的前
的前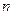 项和为
项和为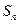 ,
,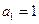 ,
,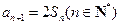 .
.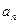 ;(Ⅱ)求数列
;(Ⅱ)求数列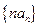 的前
的前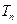 .
.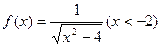 .
.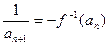 (nÎN+),求{an}的通项公式an;
(nÎN+),求{an}的通项公式an;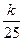 成立.若存在,求出k的值;若不存在,说明理由.
成立.若存在,求出k的值;若不存在,说明理由.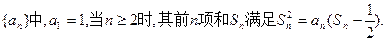
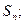 (II)设
(II)设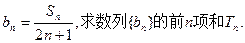
 记不超过
记不超过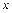 的最大整数为[
的最大整数为[ {
{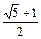 },[
},[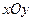 平面上有一系列的点
平面上有一系列的点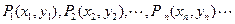 , 对于正整数
, 对于正整数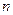 ,点
,点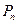 位于函数
位于函数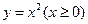 的图像上,以点
的图像上,以点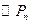 与
与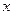 轴相切,且
轴相切,且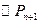 又彼此外切,若
又彼此外切,若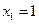 ,且
,且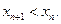
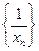 是等差数列;
是等差数列;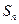 ,
,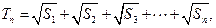 求证:
求证: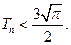
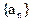 是等和数列且
是等和数列且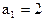 ,公和为5,那么
,公和为5,那么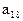 的值为_______,且这个数列前21项和
的值为_______,且这个数列前21项和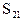 的值为_______。
的值为_______。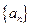 的前
的前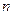 项和为
项和为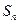 ,若
,若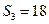 ,则
,则