题目内容
((12分)已知函数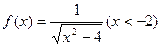 .
.
(Ⅰ) 若数列{an}的首项为a1=1,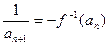 (nÎN+),求{an}的通项公式an;
(nÎN+),求{an}的通项公式an;
(Ⅱ) 设bn=an+12+an+22+¼+a2n+12,是否存在最小的正整数k,使对于任意nÎN+有bn<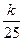 成立.若存在,求出k的值;若不存在,说明理由.
成立.若存在,求出k的值;若不存在,说明理由.
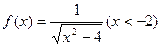 .
.(Ⅰ) 若数列{an}的首项为a1=1,
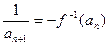 (nÎN+),求{an}的通项公式an;
(nÎN+),求{an}的通项公式an;(Ⅱ) 设bn=an+12+an+22+¼+a2n+12,是否存在最小的正整数k,使对于任意nÎN+有bn<
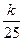 成立.若存在,求出k的值;若不存在,说明理由.
成立.若存在,求出k的值;若不存在,说明理由.(I)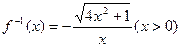 (Ⅱ)k=8
(Ⅱ)k=8
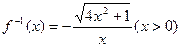 (Ⅱ)k=8
(Ⅱ)k=8解:(Ⅰ)∵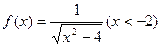 ,∴
,∴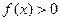 由y=
由y=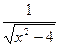 解得:
解得: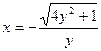 ∴
∴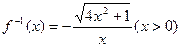 …(3分)
…(3分)
(Ⅱ)由题意得: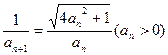 ∴
∴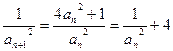
∴{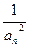 }是以
}是以 =1为首项,以4为公差的等差数列. ∴
=1为首项,以4为公差的等差数列. ∴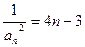 , ∴
, ∴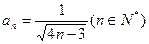 .
.
(Ⅲ)∴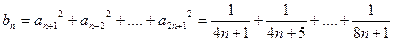
则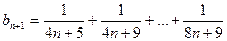
∴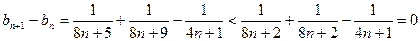
∴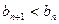 ,∴ {bn}是一单调递减数列.∴
,∴ {bn}是一单调递减数列.∴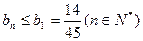 ,要使
,要使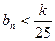 ,则
,则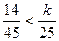 ,
,
∴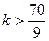 又kÎN* ,∴k³8 ,∴kmin=8即存在最小的正整数k=8,使得
又kÎN* ,∴k³8 ,∴kmin=8即存在最小的正整数k=8,使得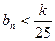 …(12分)
…(12分)
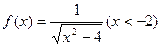 ,∴
,∴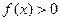 由y=
由y=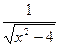 解得:
解得: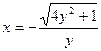 ∴
∴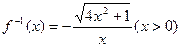 …(3分)
…(3分) (Ⅱ)由题意得:
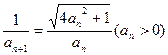 ∴
∴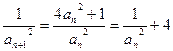
∴{
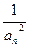 }是以
}是以 =1为首项,以4为公差的等差数列. ∴
=1为首项,以4为公差的等差数列. ∴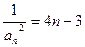 , ∴
, ∴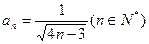 .
. (Ⅲ)∴
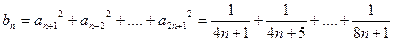
则
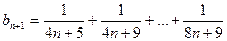
∴
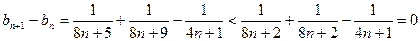
∴
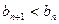 ,∴ {bn}是一单调递减数列.∴
,∴ {bn}是一单调递减数列.∴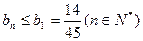 ,要使
,要使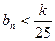 ,则
,则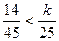 ,
,∴
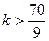 又kÎN* ,∴k³8 ,∴kmin=8即存在最小的正整数k=8,使得
又kÎN* ,∴k³8 ,∴kmin=8即存在最小的正整数k=8,使得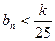 …(12分)
…(12分)
练习册系列答案
 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案
相关题目
 中,
中,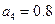 ,
,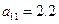 ,则
,则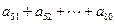 =
=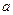 吨,按计划正式运营后的第一年进油量为已储油量的25%,以后每年的进油量均为上一年底储油量的25%,且每年年内用出
吨,按计划正式运营后的第一年进油量为已储油量的25%,以后每年的进油量均为上一年底储油量的25%,且每年年内用出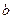 吨,设
吨,设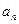 为正式运营后第
为正式运营后第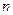 年年底的石油储量.(Ⅰ)求
年年底的石油储量.(Ⅰ)求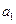 、
、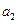 、
、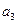 ; (Ⅱ)猜测出
; (Ⅱ)猜测出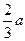 吨,如果
吨,如果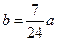 吨,该油库能否长期按计划运营?如果能,请加以证明;如果不能,请说明理由.(计算中可供参考的数据:
吨,该油库能否长期按计划运营?如果能,请加以证明;如果不能,请说明理由.(计算中可供参考的数据: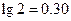 ,
,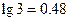 )
) 中,
中, ,
, 为其前
为其前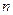 项的和,满足
项的和,满足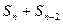 =
=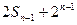
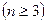 ,令
,令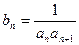 (Ⅰ)求数列
(Ⅰ)求数列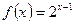 ,求证:
,求证: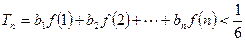 (Ⅲ)设
(Ⅲ)设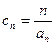 ,求证数列
,求证数列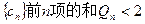
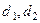 为公差的等差数列
为公差的等差数列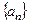 ,
,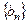 ,满足
,满足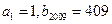 .(Ⅰ)若
.(Ⅰ)若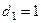 ,且存在正整数
,且存在正整数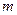 ,使得
,使得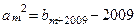 ,求
,求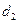 的最小值;(Ⅱ)若
的最小值;(Ⅱ)若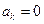 ,
,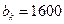 且数列
且数列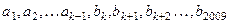 ,的前项
,的前项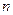 和
和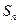 满足
满足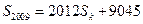 ,求
,求 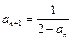 ,(1)求证数列
,(1)求证数列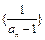 为等差数列,并求出公差;(2)设数列{an}的前n项和为Sn,证明Sn<n-ln(n+1);(3)设
为等差数列,并求出公差;(2)设数列{an}的前n项和为Sn,证明Sn<n-ln(n+1);(3)设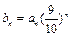 ,证明:对任意正整数n,m,都有
,证明:对任意正整数n,m,都有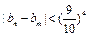 .
.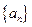 的前
的前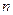 项和为
项和为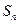 ,
, 为非零常数.已知对任意正整数
为非零常数.已知对任意正整数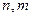 ,当
,当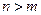 时,
时,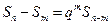 总成立.
总成立.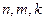 成等差数列,求证:
成等差数列,求证: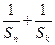 ≥
≥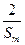 .
.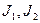 是数据入口,C是计算结果出口,计算过程是:由
是数据入口,C是计算结果出口,计算过程是:由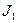 输入任意固定的正整数,
输入任意固定的正整数,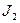 输入的正整数增加1,则输出的结果比原来增加2;③若
输入的正整数增加1,则输出的结果比原来增加2;③若