题目内容
(本小题满分14分)
在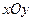 平面上有一系列的点
平面上有一系列的点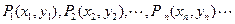 , 对于正整数
, 对于正整数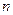 ,点
,点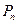 位于函数
位于函数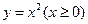 的图像上,以点
的图像上,以点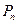 为圆心的
为圆心的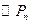 与
与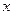 轴相切,且
轴相切,且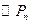 与
与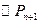 又彼此外切,若
又彼此外切,若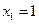 ,且
,且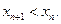
(1)求证:数列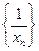 是等差数列;
是等差数列;
(2)设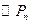 的面积为
的面积为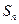 ,
,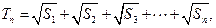 求证:
求证: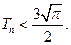
在
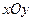 平面上有一系列的点
平面上有一系列的点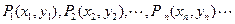 , 对于正整数
, 对于正整数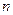 ,点
,点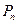 位于函数
位于函数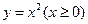 的图像上,以点
的图像上,以点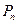 为圆心的
为圆心的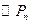 与
与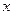 轴相切,且
轴相切,且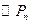 与
与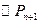 又彼此外切,若
又彼此外切,若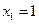 ,且
,且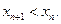
(1)求证:数列
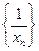 是等差数列;
是等差数列;(2)设
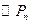 的面积为
的面积为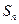 ,
,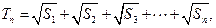 求证:
求证: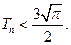
解:(1)证明: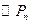 的半径为
的半径为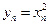 ,
,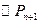 的半径为
的半径为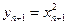 ,………1分
,………1分
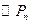 和
和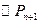 两圆相外切,则
两圆相外切,则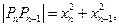 …………………………2分
…………………………2分
即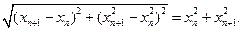 ………………3分
………………3分
整理,得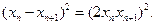 ………………5分
………………5分
又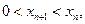 所以
所以 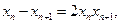 ………………………………6分
………………………………6分
即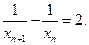 故数列
故数列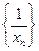 是等差数列 ………………………………7分
是等差数列 ………………………………7分
(2)由(1)得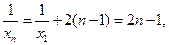 即
即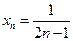 , ………………8分
, ………………8分
又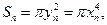 所以
所以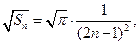 ………………………9分
………………………9分
法(一):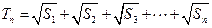
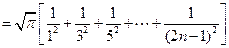 ………………11分
………………11分
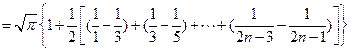 ……13分
……13分
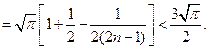 ………………………………14分
………………………………14分
法(二):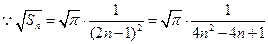
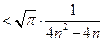
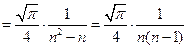 ………………10分
………………10分
 …………………………………………11分
…………………………………………11分
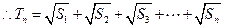
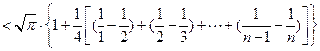 ……………12分
……………12分
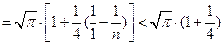 ……………………………13分
……………………………13分
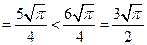 …………………………………………14分
…………………………………………14分
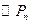 的半径为
的半径为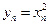 ,
,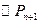 的半径为
的半径为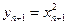 ,………1分
,………1分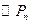 和
和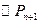 两圆相外切,则
两圆相外切,则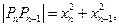 …………………………2分
…………………………2分即
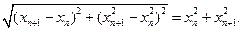 ………………3分
………………3分整理,得
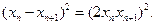 ………………5分
………………5分又
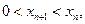 所以
所以 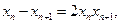 ………………………………6分
………………………………6分即
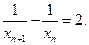 故数列
故数列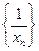 是等差数列 ………………………………7分
是等差数列 ………………………………7分(2)由(1)得
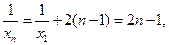 即
即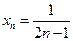 , ………………8分
, ………………8分又
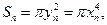 所以
所以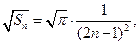 ………………………9分
………………………9分法(一):
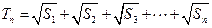
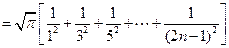 ………………11分
………………11分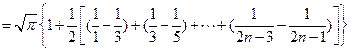 ……13分
……13分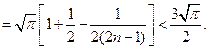 ………………………………14分
………………………………14分法(二):
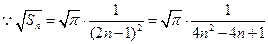
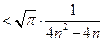
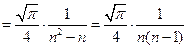 ………………10分
………………10分 …………………………………………11分
…………………………………………11分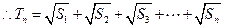
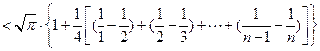 ……………12分
……………12分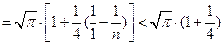 ……………………………13分
……………………………13分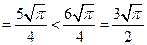 …………………………………………14分
…………………………………………14分
练习册系列答案
 出彩同步大试卷系列答案
出彩同步大试卷系列答案
相关题目

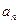 ▲ .
▲ .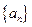 的前
的前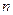 项和为
项和为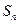 ,
, 为非零常数.已知对任意正整数
为非零常数.已知对任意正整数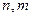 ,当
,当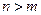 时,
时,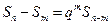 总成立.
总成立.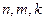 成等差数列,求证:
成等差数列,求证: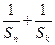 ≥
≥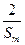 .
.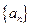 前
前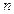 项和为
项和为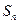 ,已知对任意的
,已知对任意的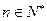 ,点
,点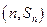 在二次函数
在二次函数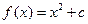 图象上。
图象上。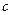 ,
,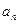 ;
;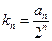 ,求数列
,求数列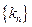 前
前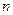 项和
项和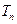 .
.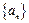 的各项均是正数,其前
的各项均是正数,其前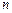 项和为
项和为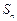 ,满足
,满足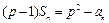 ,其中
,其中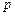 为正常数,且
为正常数,且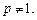
 (1)求数列
(1)求数列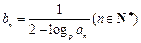 ,数列
,数列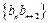 的前
的前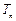 ,求证:
,求证: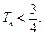
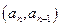 在直线
在直线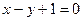 上,
上, 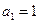 ,
,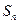 是数列
是数列 的前n项和,数列
的前n项和,数列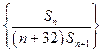 的最大值为
的最大值为 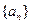 的前
的前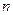 项和为
项和为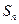 ,且
,且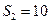 ,
,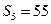 ,则过点
,则过点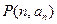 和
和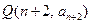
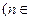 N*)的直线的斜率是__________。
N*)的直线的斜率是__________。