题目内容
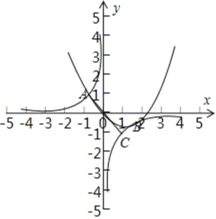
【题目】设函数
，g（x）=x2+bx，若y=f（x）的图象与y=g（x）的图象有且仅有两个不同的公共点A（x1，y1），B（x2，y2），则下列判断正确的是（ ）
A.
,
B.,
C.
,D.,
【答案】A
【解析】
作出两函数图象，根据图象的对称关系得出答案．
解：函数
，g（x）=x2+bx，
在同一坐标系中分别画出两个函数的图象，
∴f（x）与g（x）在第二象限必有一个公共点，不妨设为A（x1，y1），
∵f（x）与g（x）有且仅有两个不同的公共点，
∴g（x）与f（x）在第四象限相切，不妨设切点为B（x2，y2），
作出点A关于原点的对称点C，则C点坐标为（-x1，-y1），
由图象知-x1＜x2，-y1＜y2，即x1+x2＞0，y1+y2＞0，
故选：A．
【题目】随着我国经济的发展，居民的储蓄存款逐年增长。设某地区城乡居民人民币储蓄存款
（单位：亿元）的数据如下：
年份 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 | 2018 |
年份代号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
储蓄存款 | 3.4 | 3.6 | 4.5 | 4.9 | 5.5 | 6.1 | 7.0 |
（1）求关于
的线性回归方程；
（2）2018年城乡居民储蓄存款前五名中，有三男和两女。现从这5人中随机选出2人参加某访谈节目，求选中的2人性别不同的概率。
附：回归直线的斜率和截距的最小二乘估计公式分别为：
，
。
【题目】某单位有2000名职工，老年、中年、青年分布在管理、技术开发、营销、生产各部门中，如下表所示：
人数 | 管理 | 技术开发 | 营销 | 生产 | 共计 |
老年 | 40 | 40 | 40 | 80 | 200 |
中年 | 80 | 120 | 160 | 240 | 600 |
青年 | 40 | 160 | 280 | 720 | 1 200 |
小计 | 160 | 320 | 480 | 1 040 | 2 000 |
(1)若要抽取40人调查身体状况，则应怎样抽样？
(2)若要开一个25人的讨论单位发展与薪金调整方面的座谈会，则应怎样抽选出席人？
