Question

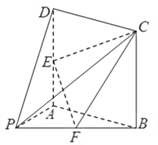
【题目】如图，在平面直角坐标系中，已知：，椭圆：，为椭圆右顶点.过原点且异于坐标轴的直线与椭圆交于，两点，直线与的另一交点为，直线与的另一交点为，其中.设直线，的斜率分别为，.

（Ⅰ）求的值；

（Ⅱ）记直线，的斜率分别为，，是否存在常数，使得？若存在，求值；若不存在，说明理由.

Answer 1

【答案】(1)见解析；（2）见解析.

【解析】

设，代入椭圆方程，运用直线的斜率公式，化简即可求出答案

通过联立直线的方程和圆的方程求出点的坐标，然后联立直线的方程和椭圆的方程求出点的坐标，再求直线和直线的斜率，看是否两个斜率之间有关系，即可得证

（Ⅰ）设则，且，

∴ k1k2＝·＝＝＝－.

（Ⅱ）解　由题意得直线AP的方程为y＝k1(x－2)，联立

得(1＋k)x2－4kx＋4(k－1)＝0，设P(xp，yp)，

解得xp＝，yp＝k1(xp－2)＝，

联立得(1＋4k)x2－16kx＋4(4k－1)＝0，设B(xB，yB)，

解得xB＝，yB＝k1(xB－2)＝，

∴kBC＝＝，kPQ＝＝＝，

∴kPQ＝kBC，故存在常数λ＝，使得kPQ＝kBC，