题目内容
如图,在四棱锥O-ABCD中,底面ABCD是边长为1的菱形,∠ABC=45°,OA⊥底面ABCD,OA=2,M为OA的中点.
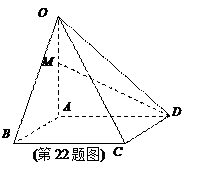
(1)求异面直线AB与MD所成角的大小;
(2)求平面OAB与平面OCD所成二面角的余弦值.
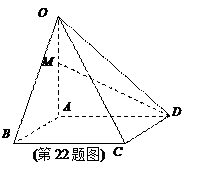
(1)求异面直线AB与MD所成角的大小;
(2)求平面OAB与平面OCD所成二面角的余弦值.
略
解:作AP⊥CD于点P,分别以AB、AP、AO所在直线为x、y、z轴建立坐标系,则A(0,0,0),B(1,0,0),P(0,,0),D(-,,0),O(0,0,2),M(0,0,1).
(1)=(1,0,0),=(-,,-1),则cos<,>=-,故AB与MD所成角为. …………………4分
(2)=(0,,-2),=(-,,-2),
设平面OCD法向量n=(x,y,z),则n·=0,n·=0,
即,取z=,则n=(0,4,). ……………………6分
易得平面OAB的一个法向量为m=(0,1,0),
cos<n,m>=, ……………………9分
故平面OAB与平面OCD所成二面角的平面角余弦值为.………………10分
|
|
(2)=(0,,-2),=(-,,-2),
设平面OCD法向量n=(x,y,z),则n·=0,n·=0,
即,取z=,则n=(0,4,). ……………………6分
易得平面OAB的一个法向量为m=(0,1,0),
cos<n,m>=, ……………………9分
故平面OAB与平面OCD所成二面角的平面角余弦值为.………………10分

练习册系列答案
相关题目
 中,底面
中,底面 是菱形,
是菱形,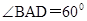 ,
,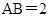 ,
,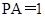 ,
,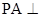 平面
平面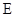 是
是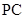 的中点,
的中点,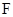 是
是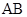 的中点.
的中点. 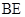 ∥平面
∥平面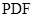 ;
;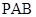 ;
;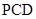 所成的锐二面角的大小.
所成的锐二面角的大小.
 Ⅱ)求证:EF∥平面PAB;
Ⅱ)求证:EF∥平面PAB;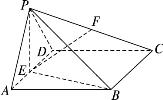
 的棱长为
的棱长为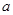 ,那么四面体
,那么四面体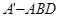 的体积是:
的体积是: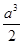
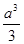
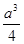
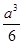
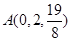 ,
,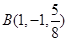 ,
,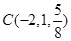 是平面
是平面 内的三点,设平面
内的三点,设平面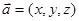 ,则
,则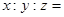
 中,
中,
 则
则 的长为 .
的长为 . -A1B1C1中.∠ BAC=90°,AB=AC=AA1 =1.D是棱CC1上的一
-A1B1C1中.∠ BAC=90°,AB=AC=AA1 =1.D是棱CC1上的一 A.
A.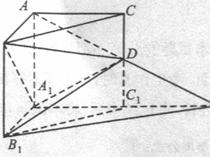
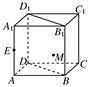
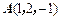 关于面
关于面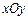 的对称点为
的对称点为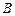 ,C(1,-2,-1),则
,C(1,-2,-1),则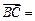 __ ____
__ ____