题目内容
如图,在四棱锥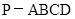 中,底面
中,底面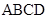 是菱形,
是菱形,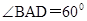 ,
,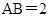 ,
,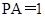 ,
,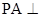 平面
平面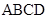 ,
,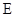 是
是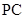 的中点,
的中点,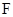 是
是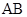 的中点.
的中点.
(Ⅰ) 求证: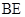 ∥平面
∥平面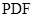 ;
;
(Ⅱ)求证:平面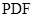 ⊥平面
⊥平面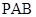 ;
;
(Ⅲ)求平面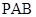 与平面
与平面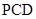 所成的锐二面角的大小.
所成的锐二面角的大小.

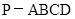 中,底面
中,底面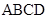 是菱形,
是菱形,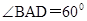 ,
,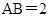 ,
,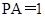 ,
,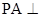 平面
平面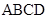 ,
,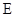 是
是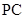 的中点,
的中点,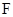 是
是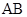 的中点.
的中点. (Ⅰ) 求证:
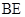 ∥平面
∥平面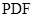 ;
;(Ⅱ)求证:平面
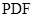 ⊥平面
⊥平面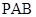 ;
;(Ⅲ)求平面
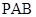 与平面
与平面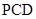 所成的锐二面角的大小.
所成的锐二面角的大小.
(Ⅰ) 取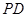 中点为
中点为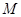 ,连
,连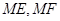 ∵
∵ 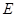 是
是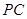 的中点 ∴
的中点 ∴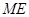 是
是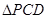 的中位线,∴
的中位线,∴ 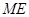
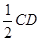 ∵
∵ 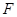 是
是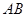 中点且
中点且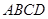 是菱形,
是菱形,
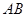
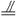
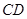 ,∴
,∴ 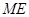
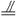
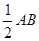 . ∴
. ∴ 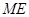
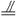
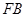
∴ 四边形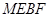 是平行四边形. 从而
是平行四边形. 从而 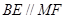 , ∵
, ∵ 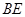
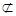 平面
平面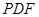 ,
,
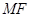
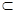 平面
平面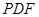 , ∴
, ∴ 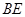 ∥平面
∥平面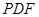 ……………………………4分
……………………………4分
(Ⅱ)∵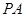 ⊥平面
⊥平面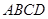 ,
,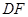
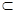 平面
平面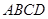 ∴
∴ 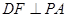
∵ 底面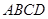 是菱形,
是菱形,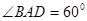 ∴
∴ 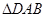 为正三角形, ∵
为正三角形, ∵ 是
是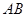 中点 ∴
中点 ∴ 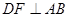 ∵
∵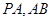 是平面
是平面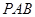 内的两条相交直线 ∴
内的两条相交直线 ∴ 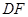 ⊥平面
⊥平面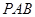 .
.
∵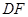
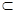 平面
平面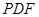 ∴ 平面
∴ 平面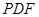 ⊥平面
⊥平面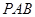 . ……………………………8分
. ……………………………8分
说明:(Ⅰ) 、(Ⅱ)前两小题用向量法,解答只要言之有理均应按步给分.
(Ⅲ)以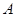 为原点,垂直于
为原点,垂直于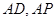 的方向为
的方向为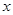 轴,
轴,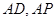 的方向分别为
的方向分别为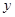 轴、
轴、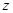 轴建立空间直角坐标系,易知
轴建立空间直角坐标系,易知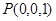 、
、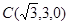 、
、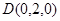 、
、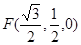 .
.
由(Ⅱ)知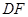 ⊥平面
⊥平面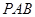 ,∴
,∴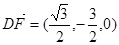 是平面
是平面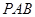 的一个法向量,
的一个法向量,
设平面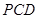 的一个法向量为
的一个法向量为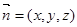
由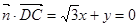 ,且由
,且由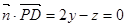
在以上二式中令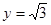 ,则得
,则得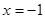 ,
,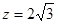 ,
,
∴ ,设平面
,设平面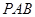 与平面
与平面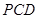 所成锐角为
所成锐角为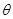
∴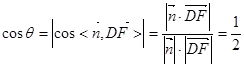 .
.
故平面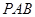 与平面
与平面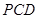 所成的锐角为
所成的锐角为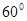
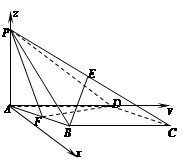
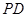 中点为
中点为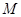 ,连
,连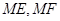 ∵
∵ 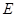 是
是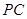 的中点 ∴
的中点 ∴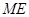 是
是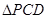 的中位线,∴
的中位线,∴ 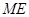
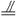
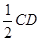 ∵
∵ 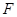 是
是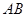 中点且
中点且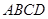 是菱形,
是菱形,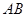
 ,∴
,∴ 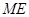
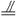
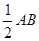 . ∴
. ∴ 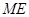
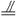
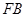
∴ 四边形
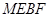 是平行四边形. 从而
是平行四边形. 从而 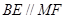 , ∵
, ∵ 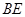
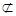 平面
平面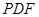 ,
,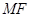
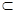 平面
平面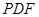 , ∴
, ∴ 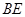 ∥平面
∥平面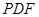 ……………………………4分
……………………………4分(Ⅱ)∵
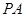 ⊥平面
⊥平面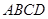 ,
,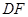
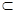 平面
平面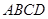 ∴
∴ 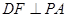
∵ 底面
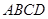 是菱形,
是菱形,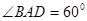 ∴
∴ 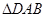 为正三角形, ∵
为正三角形, ∵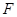 是
是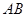 中点 ∴
中点 ∴ 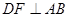 ∵
∵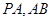 是平面
是平面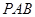 内的两条相交直线 ∴
内的两条相交直线 ∴ 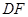 ⊥平面
⊥平面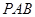 .
. ∵
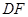
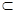 平面
平面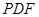 ∴ 平面
∴ 平面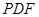 ⊥平面
⊥平面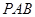 . ……………………………8分
. ……………………………8分说明:(Ⅰ) 、(Ⅱ)前两小题用向量法,解答只要言之有理均应按步给分.
(Ⅲ)以
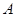 为原点,垂直于
为原点,垂直于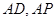 的方向为
的方向为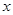 轴,
轴,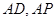 的方向分别为
的方向分别为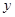 轴、
轴、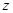 轴建立空间直角坐标系,易知
轴建立空间直角坐标系,易知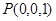 、
、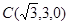 、
、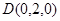 、
、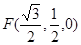 .
.由(Ⅱ)知
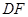 ⊥平面
⊥平面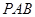 ,∴
,∴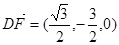 是平面
是平面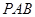 的一个法向量,
的一个法向量,设平面
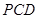 的一个法向量为
的一个法向量为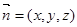
由
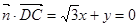 ,且由
,且由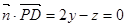
在以上二式中令
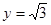 ,则得
,则得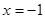 ,
,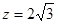 ,
,∴
 ,设平面
,设平面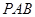 与平面
与平面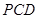 所成锐角为
所成锐角为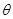
∴
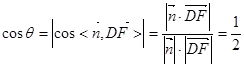 .
. 故平面
 与平面
与平面 所成的锐角为
所成的锐角为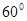
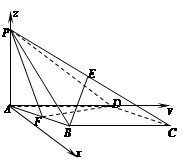
略

练习册系列答案
相关题目
 ,则MN与平面BB1C1C的位置关系是 ( ).
,则MN与平面BB1C1C的位置关系是 ( ).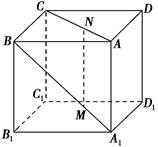
 等于( )
等于( )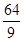
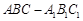 中,△ABC为等边三角形,侧棱
中,△ABC为等边三角形,侧棱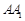 ⊥平面
⊥平面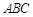 ,
,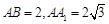 ,D、E分别为
,D、E分别为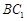 的中点.
的中点.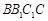 ;
;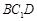 所成角;
所成角; 的体积.
的体积.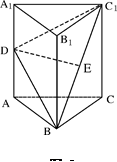
 关于坐标平面xoy及y轴的对称点的坐标分别是(a,b,c)、(e,f,d), 则c与e的和为
关于坐标平面xoy及y轴的对称点的坐标分别是(a,b,c)、(e,f,d), 则c与e的和为  ,
,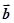 是两个单位向量,其夹角为
是两个单位向量,其夹角为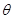 ,下面给出四个命题
,下面给出四个命题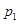 :
: ,
,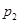 :
: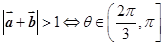 ,
, :
: ,
,  :
: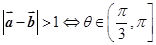 ,
,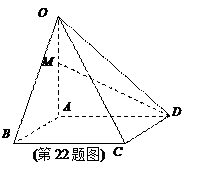
 ,则该点的坐标
,则该点的坐标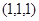
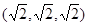
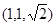
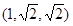
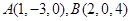 的距离是___________.
的距离是___________.