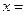题目内容
在四棱锥P-ABCD中,平面PAD⊥平面ABCD,PA=PD,底面ABCD是菱形,∠A=60°,E是AD的中点,F是PC的中点.
(Ⅰ)求证:BE⊥平面PAD;
( Ⅱ)求证:EF∥平面PAB;
Ⅱ)求证:EF∥平面PAB;
(Ⅰ)求证:BE⊥平面PAD;
(
 Ⅱ)求证:EF∥平面PAB;
Ⅱ)求证:EF∥平面PAB;
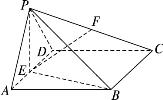
(Ⅰ)证明:∵AB=2,∴AE=1,
∴BE2=AB2+AE2-2AB·AE·cos ∠A=4+1 -2×2×1×cos 60°=3,
-2×2×1×cos 60°=3,
∴AE2+BE2=1+3=4=AB2,∴BE⊥AE.
又平面PAD⊥平面ABCD,交线为AD,
∴BE⊥平面PAD.
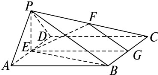
(Ⅱ)证明:取BC的中点G,连接GE,GF.则GF∥PB,EG∥AB,
又GF∩EG=G,∴平面EFG∥平面PAB,∴EF∥平面PAB.
(Ⅲ)解:∵AD∥BC,∴AD∥平面PBC.
∴点 A到平面PBC的距离等于点E到平面PBC的距离.
A到平面PBC的距离等于点E到平面PBC的距离.
因为平面PBE⊥平面PBC.
又平面PBE∩平面PBC=PB,
作EO⊥PB于O,则EO是E到平面PBC的距离,
且PE=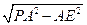 =1,BE=
=1,BE=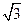 ,∴PB=2.
,∴PB=2.
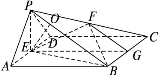
由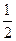 EO·PB=
EO·PB=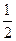 PE·EB,
PE·EB,
∴EO=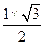 =
=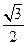 .
.
∴BE2=AB2+AE2-2AB·AE·cos ∠A=4+1
 -2×2×1×cos 60°=3,
-2×2×1×cos 60°=3,∴AE2+BE2=1+3=4=AB2,∴BE⊥AE.
又平面PAD⊥平面ABCD,交线为AD,
∴BE⊥平面PAD.

(Ⅱ)证明:取BC的中点G,连接GE,GF.则GF∥PB,EG∥AB,
又GF∩EG=G,∴平面EFG∥平面PAB,∴EF∥平面PAB.
(Ⅲ)解:∵AD∥BC,∴AD∥平面PBC.
∴点
 A到平面PBC的距离等于点E到平面PBC的距离.
A到平面PBC的距离等于点E到平面PBC的距离.因为平面PBE⊥平面PBC.
又平面PBE∩平面PBC=PB,
作EO⊥PB于O,则EO是E到平面PBC的距离,
且PE=
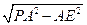 =1,BE=
=1,BE=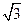 ,∴PB=2.
,∴PB=2.由
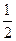 EO·PB=
EO·PB=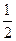 PE·EB,
PE·EB,
∴EO=
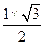 =
=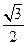 .
.略

练习册系列答案
相关题目
 等于( )
等于( )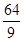
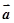 ,
,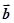 是两个单位向量,其夹角为
是两个单位向量,其夹角为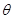 ,下面给出四个命题
,下面给出四个命题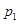 :
: ,
,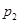 :
: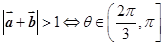 ,
,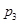 :
: ,
, 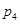 :
: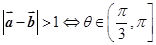 ,
,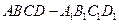 中,
中, ,
,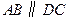 ,
,
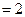 .
. 平面
平面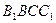 ;
;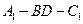 的余弦值.
的余弦值.
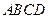 是边
是边 长为1的正方形,
长为1的正方形,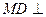 平面
平面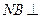 平面
平面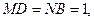
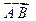 方向为侧视方向,侧视图是什么形状?说明理由并画出侧视图。
方向为侧视方向,侧视图是什么形状?说明理由并画出侧视图。
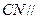 平面
平面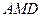 ;
;
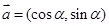 ,
,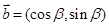 ,其中
,其中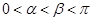 .
. 与
与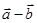 互相垂直;
互相垂直;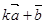 与
与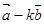 的长度相等,求
的长度相等,求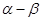 的值(
的值(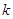 为非零的常数).
为非零的常数).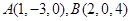 的距离是___________.
的距离是___________.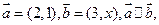 则
则