题目内容
已知抛物线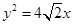 的焦点为椭圆
的焦点为椭圆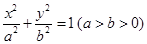 的右焦点,且椭圆的长轴长为4,M、N是椭圆上的的动点.
的右焦点,且椭圆的长轴长为4,M、N是椭圆上的的动点.
(1)求椭圆标准方程;
(2)设动点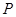 满足:
满足: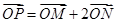 ,直线
,直线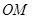 与
与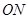 的斜率之积为
的斜率之积为 ,证明:存在定点
,证明:存在定点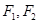 使
使
得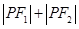 为定值,并求出
为定值,并求出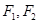 的坐标;
的坐标;
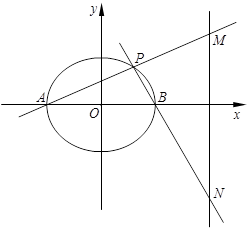
(3)若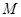 在第一象限,且点
在第一象限,且点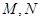 关于原点对称,
关于原点对称,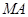 垂直于
垂直于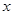 轴于点
轴于点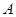 ,连接
,连接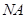 并延长交椭圆于点
并延长交椭圆于点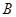 ,记直线
,记直线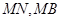 的斜率分别为
的斜率分别为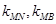 ,证明:
,证明: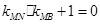 .
.
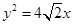 的焦点为椭圆
的焦点为椭圆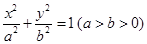 的右焦点,且椭圆的长轴长为4,M、N是椭圆上的的动点.
的右焦点,且椭圆的长轴长为4,M、N是椭圆上的的动点.(1)求椭圆标准方程;
(2)设动点
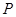 满足:
满足: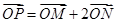 ,直线
,直线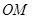 与
与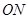 的斜率之积为
的斜率之积为 ,证明:存在定点
,证明:存在定点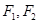 使
使得
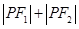 为定值,并求出
为定值,并求出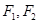 的坐标;
的坐标;(3)若
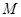 在第一象限,且点
在第一象限,且点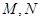 关于原点对称,
关于原点对称,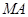 垂直于
垂直于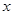 轴于点
轴于点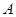 ,连接
,连接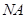 并延长交椭圆于点
并延长交椭圆于点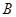 ,记直线
,记直线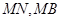 的斜率分别为
的斜率分别为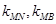 ,证明:
,证明: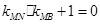 .
.(1) ;(2)存在
;(2)存在 使得
使得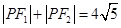 ;(3)证明过程详见试题解析.
;(3)证明过程详见试题解析.
 ;(2)存在
;(2)存在 使得
使得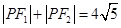 ;(3)证明过程详见试题解析.
;(3)证明过程详见试题解析.试题分析:(1)由双曲线
 的焦点与椭圆
的焦点与椭圆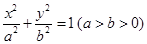 的焦点重合求出椭圆中的
的焦点重合求出椭圆中的 ,再由
,再由 ,求出所求椭圆方程为
,求出所求椭圆方程为 ;(2)先设
;(2)先设 ,由
,由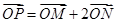 ,结合椭圆的标准方程可以得到
,结合椭圆的标准方程可以得到 使得
使得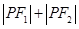 为定值;(3)要证明
为定值;(3)要证明 就是要考虑
就是要考虑 ,详见解析.
,详见解析.试题解析:(1)由题设可知:因为抛物线
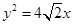 的焦点为
的焦点为 ,
, 所以椭圆中的
 又由椭圆的长轴为4得
又由椭圆的长轴为4得
故

故椭圆的标准方程为:

(2)设
 ,
,由
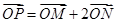 可得:
可得:
由直线OM与ON的斜率之积为
 可得:
可得: ,即
,即
由①②可得:


M、N是椭圆上的点,故

故
 ,即
,即
由椭圆定义可知存在两个定点
 ,
,使得动点P到两定点距离和为定值
 ;
; (3)设
 ,由题设可知
,由题设可知
 ,
, 由题设可知
 斜率存在且满足
斜率存在且满足 .
.
将③代入④可得:

 ⑤
⑤点
 在椭圆
在椭圆 ,
,故



练习册系列答案
 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案 ABC考王全优卷系列答案
ABC考王全优卷系列答案
相关题目
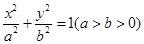 的一个焦点
的一个焦点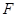 与抛物线
与抛物线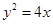 的焦点重合,且截抛物线的准线所得弦长为
的焦点重合,且截抛物线的准线所得弦长为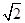 ,倾斜角为
,倾斜角为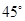 的直线
的直线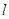 过点
过点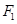 ,问抛物线
,问抛物线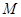 ,使得
,使得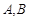 分别是椭圆
分别是椭圆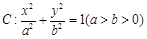 的左,右顶点,点
的左,右顶点,点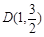 在椭圆
在椭圆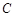 上,且直线
上,且直线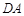 与直线
与直线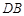 的斜率之积为
的斜率之积为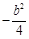 .
.
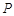 为椭圆
为椭圆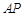 ,
,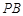 与椭圆的右准线分别交于点
与椭圆的右准线分别交于点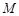 ,
,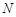 .
.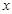 轴上是否存在一个定点
轴上是否存在一个定点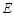 ,使得
,使得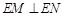 ?若存在,求点
?若存在,求点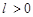 ,求
,求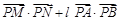 的取值范围.
的取值范围. 的焦点分别为
的焦点分别为 和
和 ,点
,点 在椭圆上,如果线段
在椭圆上,如果线段 的中点在
的中点在 轴上,那么
轴上,那么 。
。 +cos
+cos ,g(x)=2sin2
,g(x)=2sin2 .
. ,求g(α)的值;
,求g(α)的值; ·
· =
= ,则点P的轨迹是( )
,则点P的轨迹是( ) ,0),D(
,0),D( +y2=1上的动点,则
+y2=1上的动点,则 +
+ 的最小值为________.
的最小值为________.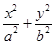 =1(a>b>0)的左、右焦点分别是F1、F2,过F1作倾斜角为45°的直线与椭圆的一个交点为M,若MF2垂直于x轴,则椭圆的离心率为________.
=1(a>b>0)的左、右焦点分别是F1、F2,过F1作倾斜角为45°的直线与椭圆的一个交点为M,若MF2垂直于x轴,则椭圆的离心率为________. 分别是椭圆为
分别是椭圆为 :
:
 的左、右焦点,过点
的左、右焦点,过点 作
作 轴的垂线交椭圆
轴的垂线交椭圆 ,过点
,过点 作直线
作直线 的垂线交直线
的垂线交直线 于点
于点 ,若直线
,若直线 与双曲线
与双曲线 的一条渐近线平行,则椭圆的离心率为( )
的一条渐近线平行,则椭圆的离心率为( )


