题目内容
已知椭圆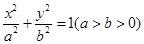 的一个焦点
的一个焦点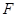 与抛物线
与抛物线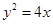 的焦点重合,且截抛物线的准线所得弦长为
的焦点重合,且截抛物线的准线所得弦长为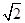 ,倾斜角为
,倾斜角为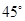 的直线
的直线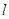 过点
过点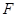 .
.
(1)求该椭圆的方程;
(2)设椭圆的另一个焦点为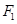 ,问抛物线
,问抛物线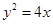 上是否存在一点
上是否存在一点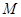 ,使得
,使得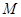 与
与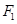 关于直线
关于直线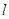 对称,若存在,求出点
对称,若存在,求出点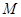 的坐标,若不存在,说明理由.
的坐标,若不存在,说明理由.
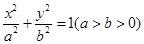 的一个焦点
的一个焦点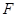 与抛物线
与抛物线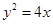 的焦点重合,且截抛物线的准线所得弦长为
的焦点重合,且截抛物线的准线所得弦长为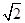 ,倾斜角为
,倾斜角为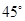 的直线
的直线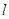 过点
过点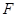 .
.(1)求该椭圆的方程;
(2)设椭圆的另一个焦点为
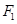 ,问抛物线
,问抛物线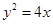 上是否存在一点
上是否存在一点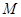 ,使得
,使得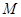 与
与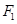 关于直线
关于直线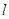 对称,若存在,求出点
对称,若存在,求出点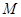 的坐标,若不存在,说明理由.
的坐标,若不存在,说明理由.(1)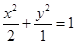 ;(2)抛物线
;(2)抛物线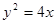 上存在一点
上存在一点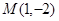 ,使得
,使得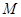 与
与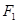 关于直线
关于直线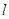 对称.
对称.
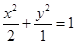 ;(2)抛物线
;(2)抛物线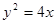 上存在一点
上存在一点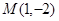 ,使得
,使得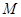 与
与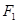 关于直线
关于直线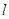 对称.
对称.试题分析:(1)求椭圆的方程,可利用待定系数法求出
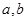 的值即可,首先确定抛物线
的值即可,首先确定抛物线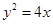 的焦点
的焦点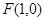 与准线方程为
与准线方程为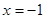 ,利用椭圆焦点
,利用椭圆焦点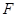 与抛物线
与抛物线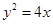 的焦点重合,得
的焦点重合,得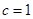 ,且截抛物线的准线所得弦长为
,且截抛物线的准线所得弦长为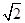 ,得交点为
,得交点为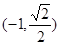 ,建立方程,求出
,建立方程,求出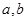 的值,即可求得椭圆的方程;(2)根据倾斜角为
的值,即可求得椭圆的方程;(2)根据倾斜角为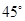 的直线
的直线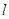 过点
过点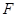 ,可得直线
,可得直线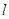 的方程
的方程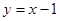 ,由(1)知椭圆的另一个焦点为
,由(1)知椭圆的另一个焦点为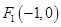 ,利用
,利用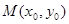 与
与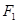 关于直线
关于直线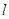 对称,利用对称,可求得
对称,利用对称,可求得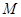 的坐标,由此可得结论.
的坐标,由此可得结论.试题解析:(1)抛物线
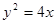 的焦点为
的焦点为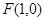 ,准线方程为
,准线方程为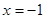 ,
,∴
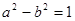 ① 2分
① 2分又椭圆截抛物线的准线
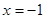 所得弦长为
所得弦长为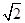 ,
,∴ 得上交点为
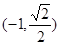 ,∴
,∴ 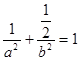 ② 4分
② 4分由①代入②得
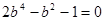 ,解得
,解得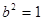 或
或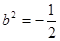 (舍去),
(舍去),从而
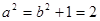
∴该椭圆的方程为该椭圆的方程为
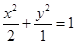 6分
6分(2)∵ 倾斜角为
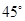 的直线
的直线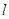 过点
过点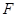 ,
,∴ 直线
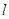 的方程为
的方程为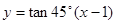 ,即
,即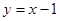 , 7分
, 7分由(1)知椭圆的另一个焦点为
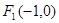 ,设
,设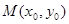 与
与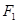 关于直线
关于直线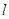 对称,则得
对称,则得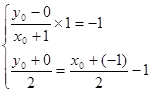 , 9分
, 9分解得
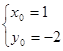 ,即
,即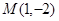 , 2分
, 2分又
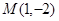 满足
满足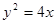 ,故点
,故点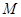 在抛物线上。所以抛物线
在抛物线上。所以抛物线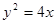 上存在一点
上存在一点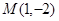 ,使得
,使得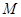 与
与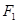 关于直线
关于直线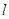 对称。 13分
对称。 13分
练习册系列答案
相关题目
 的中心在坐标原点,焦点在
的中心在坐标原点,焦点在 轴上且过点
轴上且过点 ,离心率是
,离心率是 .
. 的标准方程;
的标准方程; 且与椭圆
且与椭圆 ,
, 两点,若
两点,若 ,求直线的方程.
,求直线的方程.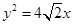 的焦点为椭圆
的焦点为椭圆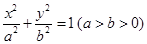 的右焦点,且椭圆的长轴长为4,M、N是椭圆上的的动点.
的右焦点,且椭圆的长轴长为4,M、N是椭圆上的的动点.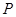 满足:
满足: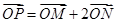 ,直线
,直线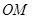 与
与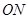 的斜率之积为
的斜率之积为 ,证明:存在定点
,证明:存在定点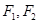 使
使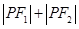 为定值,并求出
为定值,并求出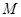 在第一象限,且点
在第一象限,且点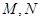 关于原点对称,
关于原点对称,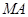 垂直于
垂直于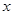 轴于点
轴于点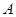 ,连接
,连接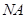 并延长交椭圆于点
并延长交椭圆于点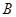 ,记直线
,记直线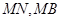 的斜率分别为
的斜率分别为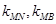 ,证明:
,证明: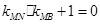 .
. +
+ =1(a>b>0)的左焦点F1作x轴的垂线交椭圆于点P,F2为右焦点,若∠F1PF2=60°,则椭圆的离心率为( )
=1(a>b>0)的左焦点F1作x轴的垂线交椭圆于点P,F2为右焦点,若∠F1PF2=60°,则椭圆的离心率为( )



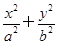 =1(a>b>0)的两个焦点分别为F1,F2,离心率为
=1(a>b>0)的两个焦点分别为F1,F2,离心率为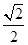 ,且过点(2,
,且过点(2,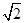 ).
).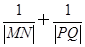 为定值.
为定值. .
. =2
=2 ,求△AOB的面积.
,求△AOB的面积.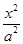 +
+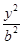 =1(a>b>0)的离心率e=
=1(a>b>0)的离心率e=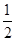 ,右焦点为F(c,0),方程ax2+2bx+c=0的两个实数根分别是x1和x2,则点P(x1,x2)到原点的距离为( )
,右焦点为F(c,0),方程ax2+2bx+c=0的两个实数根分别是x1和x2,则点P(x1,x2)到原点的距离为( )


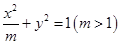 和双曲线
和双曲线 有相同的焦点
有相同的焦点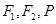 是它们的一个交点,则
是它们的一个交点,则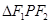 的形状是( )
的形状是( )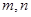 的变化而变化
的变化而变化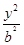 =1(0<b<1)的左、右焦点,过F1的直线l与E相交于A,B两点,且|AF2|,|AB|,|BF2|成等差数列.
=1(0<b<1)的左、右焦点,过F1的直线l与E相交于A,B两点,且|AF2|,|AB|,|BF2|成等差数列.