题目内容
椭圆
的焦点分别为
和
，点
在椭圆上，如果线段
的中点在
轴上，那么
。
的焦点分别为和，点在椭圆上，如果线段的中点在轴上，那么 。
试题分析：依题意，可求得a=2
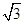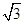，b=，c=3，设P的坐标为（x，y），由线段PF1的中点在y轴上，可求得P（3，±
），继而可求得|PF1|与|PF2|，利用余弦定理即可求得答案．
练习册系列答案
阅读快车系列答案
相关题目
试题分析：依题意，可求得a=2
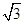，b=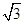，c=3，设P的坐标为（x，y），由线段PF1的中点在y轴上，可求得P（3，±），继而可求得|PF1|与|PF2|，利用余弦定理即可求得答案．阅读快车系列答案
是椭圆
的两个焦点，
为坐标原点，点
在椭圆上，且
，⊙
为直径的圆，直线
：
与⊙
，且满足
时，求弦长
的取值范围．
的中心在坐标原点，焦点在
轴上且过点
，离心率是
．
的标准方程；
且与椭圆
，
两点，若
，求直线的方程.
、
，若动点
满足
．
的方程；
，使点
的距离最小．
的焦点为椭圆
的右焦点,且椭圆的长轴长为4，M、N是椭圆上的的动点.
满足：
，直线
与
的斜率之积为
，证明：存在定点
使
为定值，并求出
在第一象限，且点
关于原点对称，
垂直于
轴于点
，连接
并延长交椭圆于点
，记直线
的斜率分别为
，证明：
.
+
=1(a>b>0)的左、右焦点,P为直线x=
上一点,△F2PF1是底角为30°的等腰三角形,则E的离心率为( )
＝1表示焦点在y轴上的椭圆，则实数k的取值范围是( )
