题目内容
(本题满分12分)设正项数列 的前
的前 项和
项和 ,且满足
,且满足 .
.
(Ⅰ)计算 的值,猜想
的值,猜想 的通项公式,并证明你的结论;
的通项公式,并证明你的结论;
(Ⅱ)设 是数列
是数列 的前
的前 项和,证明:
项和,证明: .
.
 的前
的前 项和
项和 ,且满足
,且满足 .
.(Ⅰ)计算
 的值,猜想
的值,猜想 的通项公式,并证明你的结论;
的通项公式,并证明你的结论;(Ⅱ)设
 是数列
是数列 的前
的前 项和,证明:
项和,证明: .
.(Ⅰ) ;
;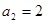 ;
; .猜想
.猜想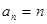 ,用数学归纳法证明;(Ⅱ)先利用数列知识求和,然后利用放缩法证明或者利用数学归纳法证明
,用数学归纳法证明;(Ⅱ)先利用数列知识求和,然后利用放缩法证明或者利用数学归纳法证明
 ;
;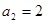 ;
; .猜想
.猜想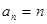 ,用数学归纳法证明;(Ⅱ)先利用数列知识求和,然后利用放缩法证明或者利用数学归纳法证明
,用数学归纳法证明;(Ⅱ)先利用数列知识求和,然后利用放缩法证明或者利用数学归纳法证明试题分析:(Ⅰ)当n=1时,
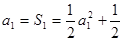 ,得
,得 ;
; ,得
,得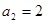 ;
;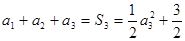 ,得
,得 .猜想
.猜想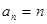 2’
2’证明:(ⅰ)当n=1时,显然成立.
(ⅱ)假设当n=k时,
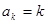 1’
1’则当n=k+1时,
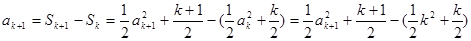
结合
 ,解得
,解得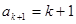 2’
2’于是对于一切的自然数
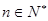 ,都有
,都有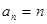 1’
1’(Ⅱ)证法一:因为
 , 3’
, 3’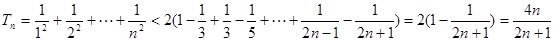 .3’
.3’证法二:数学归纳法
证明:(ⅰ)当n=1时,
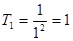 ,
,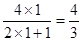 ,
,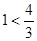 1’
1’(ⅱ)假设当n=k时,
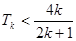 1’
1’则当n=k+1时,

要证:
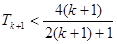
只需证:
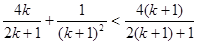
由于

所以
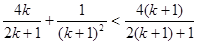 3’
3’于是对于一切的自然数
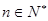 ,都有
,都有 1’
1’点评:运用数学归纳法,可以证明下列问题:与自然数n有关的恒等式、代数不等式、三角不等式、数列问题、几何问题、整除性问题等等。

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目
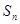 是等差数列
是等差数列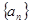 的前
的前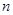 项和,若
项和,若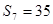 ,则
,则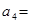 ___________。
___________。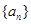 ,其前
,其前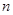 项和
项和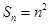 ,数列
,数列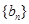 满足
满足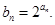
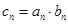 ,求数列
,求数列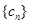 的前
的前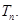
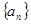 的前
的前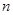 项和是
项和是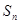 ,若
,若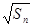 }都是等差数列,且公差相等,则
}都是等差数列,且公差相等,则
 的“分裂”中最小的数为a,而
的“分裂”中最小的数为a,而 的“分裂”中最大的数是b,则a+b= .
的“分裂”中最大的数是b,则a+b= .
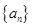 的前
的前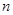 项和为
项和为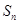 ,且方程
,且方程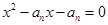 有一个根为
有一个根为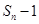 ,
,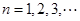 .
.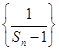 是等差数列;
是等差数列;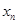 ,数列
,数列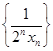 的前
的前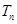 ,求
,求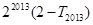 的值;
的值;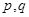 ,使得
,使得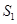 ,
,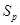 ,
,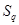 成等比数列,若存在,求出满足条件的
成等比数列,若存在,求出满足条件的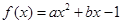 ,且不等式
,且不等式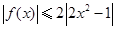 对任意的实数
对任意的实数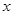 恒成立,数列
恒成立,数列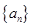 满足
满足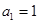 ,
,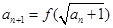
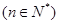 .
.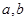 的值;
的值;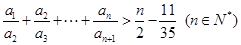 .
.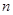 行(
行(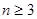 )从左向右的第3个数为
)从左向右的第3个数为 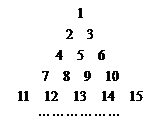
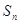 是公差不为0的等差数列
是公差不为0的等差数列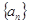 的前n项和,且
的前n项和,且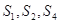 成等比数列,则
成等比数列,则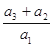 等于( )
等于( )


