题目内容
18．若不等式ax2+2ax+2＜0的解集为空集，则实数a的取值范围为0≤a≤2．分析 讨论a的取值，使不等式ax2+2ax+2＜0的解集为空集即可．
解答 解：∵不等式ax2+2ax+2＜0的解集为空集，
∴a=0时，2＜0，满足题意；
当a≠0时，$\left\{\begin{array}{l}{a＞0}\\{△≤0}\end{array}\right.$，
即$\left\{\begin{array}{l}{a＞0}\\{{4a}^{2}-4a•2≤0}\end{array}\right.$，
解得0＜a≤2；
综上，实数a的取值范围是0≤a≤2．
故答案为：0≤a≤2．
点评 本题考查了不等式恒成立的问题，解题时应对字母系数进行讨论，是基础题目．
练习册系列答案
互动课堂系列答案
激活思维智能训练课时导学练系列答案
相关题目
9．函数y=$\frac{1}{2}$x+cosx在x∈[-$\frac{π}{2}$，$\frac{π}{2}$]上的最大值为$\frac{π}{12}$+$\frac{\sqrt{3}}{2}$．
6．已知函数y=2cos（ωx+φ）（ω＞0）在区间[0，2π]的图象如图，那么ω等于（ ）
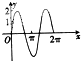
| A． | $\frac{1}{2}$ | B． | $\frac{3}{2}$ | C． | $\frac{2}{3}$ | D． | $\frac{1}{3}$ |
13．集合A={（x，y）|y=lg（x+1）-1}，B={（x，y）|x=m}，若A∩B=∅，则实数m的取值范围是（ ）
| A． | （-∞，1） | B． | （-∞，1] | C． | （-∞，-1） | D． | （-∞，-1] |