题目内容
8.已知f(x)=x2-4x+2,递增的等差数列{an}满足a1=f(x+1),a2=0,a3=f(x-1)(1)求数列{an}的通项公式;
(2)设bn=2an-2n,试求满足b1+b2+…+bn<2015的最大自然数n.
分析 (1)根据f(x)写出${a}_{1}={x}^{2}-2x-1$,${a}_{3}={x}^{2}-6x+7$,由a1+a3=0且{an}为递增数列即可求得x=1,从而根据等差数列的通项公式写出an=2n-4;
(2)写出${b}_{n}={2}^{2n-4}-2n$,根据等比数列及等差数列的求和公式即可写出${b}_{1}+{b}_{2}+…+{b}_{n}={4}^{n-2}-{n}^{2}-n$,能够说明b1+b2+…+b7<2015,而b1+b2+…+b8>2015,从而求得满足b1+b2+…+bn<2015的最大自然数n.
解答 解:(1)${a}_{1}=f(x+1)={x}^{2}-2x-1$,a2=0,${a}_{3}=f(x-1)={x}^{2}-6x+7$;
∵a1+a3=0;
∴x2-4x+3=0;
∴x=1,或3;
又{an}递增,∴x=1;
∴a1=-2,d=2;
∴an=-2+(n-1)•2=2n-4,n∈N*;
即an=2n-4,n∈N*;
(2)${b}_{n}={2}^{2n-4}-2n$;
∴b1+b2+…+bn=2-2+20+…+22n-4-(2+4+…+2n)=4n-2-n2-n;
n=7时,b1+b2+…+b7=1025-49-7<2015;
n=8时,${b}_{1}+{b}_{2}+…+{b}_{8}={4}^{6}-64-8$=4096-64-8>2015;
∴满足b1+b2+…+bn<2015的最大自然数为7.
点评 考查等差数列的定义,等差数列的通项公式,以及等比数列、等差数列的求和公式.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
20.设m,n表示两条不同直线,α,β表示两个不同的平面,下列说法正确的是( )
| A. | 若m∥β,β⊥α则m⊥α | B. | 若m⊥n,n⊥β,β⊥α,则m⊥α | ||
| C. | 若m⊥α,m⊥n则n∥α | D. | 若m⊥α,n?α,则m⊥n |
3.已知锐角α,β满足:cosα=$\frac{1}{3}$,cos(α+β)=-$\frac{1}{3}$,则cos(α-β)=( )
| A. | -$\frac{1}{2}$ | B. | $\frac{1}{2}$ | C. | -$\frac{1}{3}$ | D. | $\frac{23}{27}$ |
13.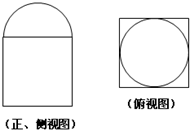 如图是某几何体的三视图(正视图与侧视图一样,上面是半径为1的半圆,下面是边长为2的正方形),则该几何体的体积是( )
如图是某几何体的三视图(正视图与侧视图一样,上面是半径为1的半圆,下面是边长为2的正方形),则该几何体的体积是( )
 如图是某几何体的三视图(正视图与侧视图一样,上面是半径为1的半圆,下面是边长为2的正方形),则该几何体的体积是( )
如图是某几何体的三视图(正视图与侧视图一样,上面是半径为1的半圆,下面是边长为2的正方形),则该几何体的体积是( )| A. | 8+$\frac{2}{3}$π | B. | 8+$\frac{4}{3}$π | C. | 24+π | D. | 20+2π |
 如图,在等腰三角形ABC中,∠B=∠C=30°,求下列事件的概率:
如图,在等腰三角形ABC中,∠B=∠C=30°,求下列事件的概率: