题目内容
16.已知椭圆C的方程为$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)离心率e=$\frac{1}{2}$,点P(2,3)在椭圆上(Ⅰ)求椭圆C的方程
(Ⅱ)求过点P的椭圆C的切线方程
(Ⅲ)若从椭圆一个焦点发出的光线照到点P被椭圆反射,证明:反射光线经过另一个焦点.
分析 (I)由题意可得:$\left\{\begin{array}{l}{\frac{c}{a}=\frac{1}{2}}\\{\frac{4}{{a}^{2}}+\frac{9}{{b}^{2}}=1}\\{{a}^{2}={b}^{2}+{c}^{2}}\end{array}\right.$,解得即可得出;
(Ⅱ)设切线l的斜率为k,可得l:y=kx-2k+3,与椭圆方程联立化为:(3+4k2)x2-8(2k-3)kx+16k2-48k-12=0,利用△=0,解出即可.
(Ⅲ)设椭圆左右焦点分别为F1(-2,0),F2(2,0),由过点P的椭圆切线方程可得:过点P的椭圆法线方程为m:2x-y-1=0,法线的方向向量$\overrightarrow{m}$=(-1,-2),只要证明$cos<\overrightarrow{P{F}_{1}},\overrightarrow{m}>$=$cos<\overrightarrow{P{F}_{2}},\overrightarrow{m}>$可得:直线PF1,F2P关于直线m对称,即可证明结论.
解答 (I)解:由题意可得:$\left\{\begin{array}{l}{\frac{c}{a}=\frac{1}{2}}\\{\frac{4}{{a}^{2}}+\frac{9}{{b}^{2}}=1}\\{{a}^{2}={b}^{2}+{c}^{2}}\end{array}\right.$,解得a2=16,b2=12,
∴椭圆C的方程为:$\frac{{x}^{2}}{16}+\frac{{y}^{2}}{12}=1$;
(Ⅱ)解:设切线l的斜率为k,∴l:y=kx-2k+3,
由$\left\{\begin{array}{l}{\frac{{x}^{2}}{16}+\frac{{y}^{2}}{12}=1}\\{y=kx-2k+3}\end{array}\right.$得:(3+4k2)x2-8(2k-3)kx+16k2-48k-12=0,
由△=64k2(2k-3)2-4(3+4k2)(16k2+48k-12)=0,
化为:4k2+4k+1=0,
解得k=-$\frac{1}{2}$.
∴求过点P的椭圆切线方程为x+2y-8=0.
(Ⅲ)证明:∵椭圆C的方程为:$\frac{{x}^{2}}{16}+\frac{{y}^{2}}{12}=1$,
设椭圆左右焦点分别为F1(-2,0),F2(2,0),
∵过点P的椭圆切线方程为x+2y-8=0,
∴过点P的椭圆法线方程为m:2x-y-1=0,
法线的方向向量$\overrightarrow{m}$=(-1,-2),
∵$\overrightarrow{P{F}_{1}}$=(-4,-3),$\overrightarrow{P{F}_{2}}$=(0,-3),
∴$cos<\overrightarrow{P{F}_{1}},\overrightarrow{m}>$=$\frac{\overrightarrow{P{F}_{1}}•\overrightarrow{m}}{|\overrightarrow{P{F}_{1}}||\overrightarrow{m}|}$=-$\frac{2}{\sqrt{5}}$,
$cos<\overrightarrow{P{F}_{2}},\overrightarrow{m}>$=$\frac{\overrightarrow{P{F}_{2}}•\overrightarrow{m}}{|\overrightarrow{P{F}_{2}}||\overrightarrow{m}|}$=$-\frac{2}{\sqrt{5}}$,
∴直线PF1,F2P关于直线m对称;
∴从椭圆一个焦点发出的光线照到点P,被椭圆反射后,反射光线一定经过另一个焦点.
点评 本题考查了椭圆的标准方程及其性质、直线与椭圆相切的性质、椭圆的光学性质、向量夹角公式、直线对称问题,考查了推理能力与计算能力,属于难题.

 应用题作业本系列答案
应用题作业本系列答案| A. | 3$\sqrt{2}$ | B. | $\sqrt{3}$ | C. | 2$\sqrt{3}$ | D. | 12 |
| A. | 3 | B. | $\sqrt{15}$ | C. | 3或5 | D. | 3或$\sqrt{15}$ |
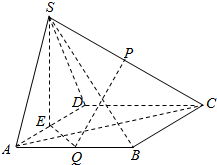 如图,在四棱锥S-ABCD中,底面ABCD为菱形,∠BAD=60°,平面SAD⊥平面ABCD,SA=SD,E,P,Q分别是棱AD,SC,AB的中点.
如图,在四棱锥S-ABCD中,底面ABCD为菱形,∠BAD=60°,平面SAD⊥平面ABCD,SA=SD,E,P,Q分别是棱AD,SC,AB的中点.