题目内容
8.若直线l:mx+ny=4和圆O:x2+y2=4没有交点,则过点(m,n)的直线与椭圆$\frac{x^2}{9}+\frac{y^2}{4}=1$的交点个数为( )| A. | 0个 | B. | 至多有一个 | C. | 1个 | D. | 2个 |
分析 通过直线与圆、圆与椭圆的位置关系可得点P(m,n)在椭圆内,进而可得结论.
解答 解:由题意可得:$\frac{|0+0-4|}{\sqrt{{m}^{2}+{n}^{2}}}$>2,即m2+n2<4,
∴点P(m,n)是在以原点为圆心,2为半径的圆内的点,
∵椭圆的长半轴3,短半轴为2,
∴圆m2+n2=4内切于椭圆,
∴点P是椭圆内的点,
∴过点P(m,n)的一条直线与椭圆的公共点数为2,
故选:D.
点评 本题考查椭圆的简单性质,注意解题方法的积累,属于中档题.

练习册系列答案
相关题目
13.设F1,F2为椭圆的两焦点,B为椭圆短轴的一个端点,若△BF1F2为正三角形,则椭圆的离心率为( )
| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | 2 |
18.圆x2+y2-2x+4y+3=0的圆心坐标为( )
| A. | (-2,4) | B. | (2,-4) | C. | (1,-2) | D. | (-1,2) |
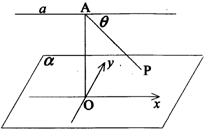 如图,已知直线a∥平面α,在平面α内有一动点P,点A是直线a上一定点,且AP与直线a所成角θ=$\frac{π}{4}$,点A到平面α的距离为2,若过点A作AO⊥α于点O,在平面α内,以过点O作直线a的平行线为x轴,以过点O作x轴的垂线为y轴建立直角坐标系,则动点P的轨迹方程为x2-y2=4..
如图,已知直线a∥平面α,在平面α内有一动点P,点A是直线a上一定点,且AP与直线a所成角θ=$\frac{π}{4}$,点A到平面α的距离为2,若过点A作AO⊥α于点O,在平面α内,以过点O作直线a的平行线为x轴,以过点O作x轴的垂线为y轴建立直角坐标系,则动点P的轨迹方程为x2-y2=4..