题目内容
19.已知f(x)是定义在[m,4m+5]上的奇函数,则m=-1,当x>0时,f(x)=lg(x+1),则当x<0时,f(x)=-lg(1-x).分析 由于奇函数的定义域必然关于原点对称,可得m+4m+5=0,即可求出m的值;
当x<0时,-x>0,由已知表达式可求得f(-x),由奇函数的性质可得f(x)与f(-x)的关系,从而可求出f(x).
解答 解:由于奇函数的定义域必然关于原点对称,由已知必有m+4m+5=0,得m=-1.
∵f(x)是R上的奇函数,当x<0时,-x>0,
∴f(-x)=lg(-x+1)=-f(x),
∴f(x)=-lg(1-x),x<0,
故答案为:-1,-lg(1-x).
点评 本题考查函数解析式的求解及奇函数的性质,属基础题

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
9.执行如图所示的程序框图,若输出i的值是11,则判断框中的横线上可以填入的最大整数为( )
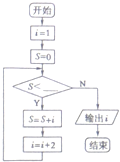

| A. | 23 | B. | 24 | C. | 25 | D. | 26 |
14.设集合A={x|x2+3x<0},B={x|x<-1},则A∩B=( )
| A. | {x|-3<x<-1} | B. | {x|-3<x<0} | C. | {x|x<-1} | D. | {x|x>0} |
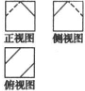 一个棱长为1的正方体沿其棱的中点截去部分后所得几何体的三视图如图所示,则该几何体的体积为$\frac{23}{24}$.
一个棱长为1的正方体沿其棱的中点截去部分后所得几何体的三视图如图所示,则该几何体的体积为$\frac{23}{24}$. 如图,在四棱锥P-ABCD中,底面ABCD是边长为1的菱形,∠BAD=60°,侧棱PA⊥底面ABCD,E是PC的中点.
如图,在四棱锥P-ABCD中,底面ABCD是边长为1的菱形,∠BAD=60°,侧棱PA⊥底面ABCD,E是PC的中点.