题目内容
【题目】已知曲线C的极坐标方程是ρ=2cos θ,以极点为平面直角坐标系的原点,极轴为x轴的正半轴,建立平面直角坐标系,直线l的参数方程是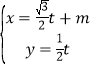 (t为参数).
(t为参数).
(1)求曲线C的直角坐标方程和直线l的普通方程;
(2)当m=2时,直线l与曲线C交于A、B两点,求|AB|的值.
【答案】(1)曲线C的直角坐标方程为(x-1)2+y2=1,直线l的普通方程为x-![]() y-m=0;
y-m=0;
(2)![]() .
.
【解析】
(1)先把曲线C的极坐标方程化为直角坐标方程,把直线的参数方程化为普通方程.(2)利用解直角三角形求直线和圆的弦长.
(1)由ρ=2cos θ,
得:ρ2=2ρcos θ,
所以x2+y2=2x,即(x-1)2+y2=1,
所以曲线C的直角坐标方程为(x-1)2+y2=1.
由 得x=
得x=![]() y+m,
y+m,
即x-![]() y-m=0,
y-m=0,
所以直线l的普通方程为x-![]() y-m=0.
y-m=0.
(2)设圆心到直线l的距离为d,
由(1)可知直线l:x-![]() y-2=0,
y-2=0,
曲线C:(x-1)2+y2=1,
圆C的圆心坐标为(1,0),半径1,
则圆心到直线l的距离为d=![]() .
.
所以|AB|=2![]() =
=![]() .
.
因此|AB|的值为![]() .
.

【题目】在对人们休闲方式的调查中,共调查了124人,其中女性70人,男性54人.女性中有43人主要的休闲方式是看电视,另外27人主要的休闲方式是运动;男性中有21人主要的休闲方式是看电视,另外33人主要的休闲方式是运动.能否在犯错误的概率不超过2.5%的前提下认为性别与休闲方式是否有关系?
| 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
【题目】在统计学中,偏差是指个别测定值与测定的平均值之差,在成绩统计时,我们把某个同学的某科考试成绩与该科班平均分的差叫某科偏差.某高二班主任为了了解学生的偏科情况,对学生数学偏差![]() (单位:分)与历史偏差
(单位:分)与历史偏差![]() (单位:分)之间的关系进行学科偏差分析,决定从全班52位同学中随机抽取一个容量为8的样本进行分析,得到他们的两科成绩偏差数据如下:
(单位:分)之间的关系进行学科偏差分析,决定从全班52位同学中随机抽取一个容量为8的样本进行分析,得到他们的两科成绩偏差数据如下:
学生序号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
数学偏差 | 20 | 15 | 13 | 3 | 2 |
|
|
|
历史偏差 |
|
|
|
|
|
|
|
|
(1)已知![]() 与
与![]() 之间具有线性相关关系,求
之间具有线性相关关系,求![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(2)若这次考试该班数学平均分为118分,历史平均分为![]() ,试预测数学成绩126分的同学的历史成绩.
,试预测数学成绩126分的同学的历史成绩.
附:参考公式与参考数据
 ,
,![]() ,
,![]() ,
,![]() .
.