Question

【题目】已知函数h（x）=lnx+ ．
（1）函数g（x）=h（2x+m），若x=1是g（x）的极值点，求m的值并讨论g（x）的单调性；
（2）函数φ（x）=h（x）﹣ +ax2﹣2x有两个不同的极值点，其极小值为M，试比较2M与﹣3的大小关系，并说明理由．

Answer 1

【答案】
（1）解：g（x）=ln（2x+m）+ ，（x＞﹣ ），

g′（x）= ﹣ = ，

若x=1是g（x）的极值点，

则g′（x）= =0，解得：m=﹣1，

故g（x）=ln（2x﹣1）+ ，（x＞ ），

g′（x）= ，

令g′（x）＞0，解得：x＞1，令g′（x）＜0，解得： ＜x＜1，

故g（x）在（ ，1）递减，在（1，+∞）递增

（2）解：φ（x）=h（x）﹣ +ax2﹣2x=ax2﹣2x+lnx（x＞0）

φ′（x）=2ax﹣2+ = （x＞0）

∵φ（x）有两个不同的极值点，

∴2ax2﹣2x+1=0在（0，+∞）有两个不同的实根．

设p（x）=2ax2﹣2x+1=0，

则 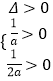，即 ，即有0＜a＜ ．

设p（x）在（0，+∞）的两根x1，x2且x1＜x2，

x	（0，x1）	x1	（x1，x2）	x2	（x2，+∞）
φ′（x）	+	0	﹣	0	+
φ（x）	递增	极大值	递减	极小值	递增

∴φ（x）的极小值为M=φ（x2）=ax22﹣2x2+lnx2

又p（x）=0在（0，+∞）的两根为x1，x2，

∴2ax22﹣2x2+1=0

∴φ（x）极小值=M=φ（x2）=ax22﹣2x2+lnx2

=x2﹣ ﹣2x2+lnx2=﹣ +lnx2﹣x2，

∴2M=﹣1+2lnx2﹣2x2，

∵x2= （0＜a＜ ）

∴x2＞1令v（x）=﹣1+2lnx﹣2x，v′（x）= ﹣2，

∴x＞1时，v′（x）＜0，v（x）在（1，+∞）递减，

∴x＞1时，v（x）=﹣1+2lnx﹣2x＜v（1）=﹣3，

∴2M＜﹣3．

【解析】（1）求出g（x）=h（x+m）的导数，根据g′（1）=0，求出m的值，从而求出g（x）的解析式，求出函数的单调区间即可；（2）对φ（x）求导数，φ（x）有两个不同的极值点，即为2ax2﹣2x+1=0在（0，+∞）有两个不同的实根．设p（x）=2ax2﹣2x+1=0，运用韦达定理和判别式，即可得到0＜a＜ ．列表得到φ（x）的单调区间和极值的关系，即可得到极小值M，令v（x）=﹣1+2lnx﹣2x，运用导数，得到v（x）在（1，+∞）递减，运用单调性即可得到2M＜﹣3．
【考点精析】解答此题的关键在于理解函数的极值与导数的相关知识，掌握求函数的极值的方法是:（1）如果在附近的左侧,右侧,那么是极大值（2）如果在附近的左侧,右侧,那么是极小值．