题目内容
【题目】已知椭圆![]() 右焦点
右焦点![]() ,离心率为
,离心率为![]() ,过
,过![]() 作两条互相垂直的弦
作两条互相垂直的弦![]() ,设
,设![]() 中点分别为
中点分别为![]() .
.

(1)求椭圆的方程;
(2) 证明:直线![]() 必过定点,并求出此定点坐标;
必过定点,并求出此定点坐标;
(3) 若弦![]() 的斜率均存在,求
的斜率均存在,求![]() 面积的最大值.
面积的最大值.
【答案】(1)![]() ;(2)直线MN过定点
;(2)直线MN过定点![]() ;(3)S△FMN的最大值为
;(3)S△FMN的最大值为![]() .
.
【解析】分析:(1)根据题意确定出c与e的值,利用离心率公式求出a的值,进而求出b的值,确定出椭圆方程即可;
(2)由直线AB与CD斜率均存在,设为k,表示出AB方程,设出A与B坐标,联立直线AB与椭圆方程,消去y得到关于x的一元二次方程,利用根与系数的关系表示出M,同理表示出N,根据M与N横坐标相同求出k的值,得到此时MN斜率不存在,直线MN恒过定点;若直线MN斜率存在,表示出直线MN斜率,进而表示出直线MN,令y=0,求出x的值,得到直线MN恒过定点,综上,得到直线MN恒过定点,求出定点坐标即可;
(3)根据P坐标,得到OP的长,由OF﹣OP表示出PF长,S△FMN=S△FPM+S△FPN,利用基本不等式求出面积的最大值即可.
详解:(1) (1)由题意:c=1, ![]() =
=![]() ,
,
∴a=![]() ,b=c=1,
,b=c=1,
则椭圆的方程为![]() +y2=1;
+y2=1;
(2) ∵AB,CD斜率均存在,
∴设直线AB方程为:y=k(x﹣1),
再设A(x1,y1),B(x2,y2),则有M(![]() ,k(
,k(![]() ﹣1)),
﹣1)),
联立得: ![]() ,
,
消去y得:(1+2k2)x2﹣4k2x+2k2﹣2=0,
∴ ,即M(
,即M(![]() ,
, ![]() ),
),
将上式中的k换成﹣![]() ,同理可得:N(
,同理可得:N(![]() ,
, ![]() ),
),
若![]() =
=![]() ,解得:k=±1,直线MN斜率不存在,
,解得:k=±1,直线MN斜率不存在,
此时直线MN过点(![]() ,0);
,0);
下证动直线MN过定点P(![]() ,0),
,0),
若直线MN斜率存在,则kMN=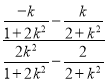 =
=![]() =
=![]() ×
×![]() ,
,
直线MN为y﹣![]() =
=![]() ×
×![]() (x﹣
(x﹣![]() ),
),
令y=0,得x=![]() +
+![]() ×
×![]() =
=![]() ×
×![]() =
=![]() ,
,
综上,直线MN过定点(![]() ,0);
,0);
(3) 由第(2)问可知直线MN过定点P(![]() ,0),
,0),
故S△FMN=S△FPM+S△FPN=![]() ×
×![]() |
|![]() |+
|+![]() ×
×![]() |
|![]() =
=![]() ×
× ,
,
令t=|k|+![]() ∈[2,+∞),S△FMN=f(t)=
∈[2,+∞),S△FMN=f(t)=![]() ×
× =
=![]() ×
×![]() ,
,
∴f(t)在t∈[2,+∞)单调递减,
当t=2时,f(t)取得最大值,即S△FMN最大值![]() ,此时k=±1.
,此时k=±1.

 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案


