题目内容
【题目】如图，在三棱锥
中，
分别是
的中点，平面
平面
，
，
是边长为2的正三角形，
.
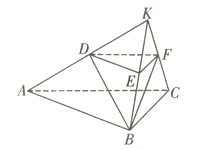
（1）求证：
平面
；
（2）求二面角
的余弦值.
【答案】（1）见解析（2）
【解析】试题分析：（1）利用空间向量，通过计算进行证明：先建立空间直角坐标系，设各点坐标，表示
，以及平面
中两相交直线
，
，利用向量数量积计算证明
，
，最后根据线面垂直判定定理得结论（2）利用方程组求出各面法向量，利用向量数量积求向量夹角余弦值，最后根据二面角与向量夹角关系确定二面角余弦值
试题解析：（Ⅰ）证明：如图，建立空间直角坐标系，则
，
，
，
得，
，
得，
CA，CK是平面KAC内的两条相交直线，
所以
平面KAC.
（Ⅱ）解：平面BDF的一个法向量
，
平面BDE（即平面ABK）的一个法向量为
，
所以二面角
的余弦值为.
练习册系列答案
相关题目
【题目】已知某产品的历史收益率的频率分布直方图如图所示.
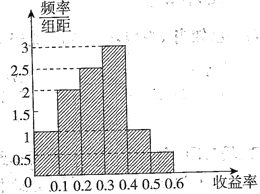
（1）试估计该产品收益率的中位数；
（2）若该产品的售价
（元）与销量
（万份）之间有较强线性相关关系，从历史销售记录中抽样得到如表5组
与
的对应数据：
售价 | 25 | 30 | 38 | 45 | 52 |
销量 | 7.5 | 7.1 | 6.0 | 5.6 | 4.8 |
根据表中数据算出
关于
的线性回归方程为
，求
的值；
（3）若从表中五组销量数据中随机抽取两组，记其中销量超过6万份的组数为
，求
的分布列及期望.