题目内容
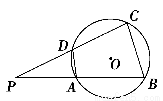
如图所示，四边形ABCD内接于⊙O，AD∶BC＝1∶2，AB＝35，PD＝40，则过点P的⊙O的切线长是________．
60
【解析】由圆内接四边形的性质定理，可得△PAD∽△PCB.∴
＝
．∴
＝
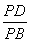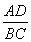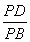，即
＝
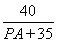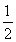，解得PA＝45.若设过点P的⊙O的切线长为x，则x2＝PA·PB＝45×80，∴x＝60.
练习册系列答案
轻巧夺冠周测月考直通中考系列答案
相关题目
轻巧夺冠周测月考直通中考系列答案题目内容
如图所示，四边形ABCD内接于⊙O，AD∶BC＝1∶2，AB＝35，PD＝40，则过点P的⊙O的切线长是________．
60
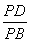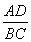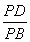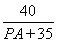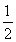【解析】由圆内接四边形的性质定理，可得△PAD∽△PCB.∴＝．∴＝，即＝，解得PA＝45.若设过点P的⊙O的切线长为x，则x2＝PA·PB＝45×80，∴x＝60.
轻巧夺冠周测月考直通中考系列答案
