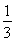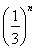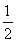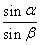题目内容
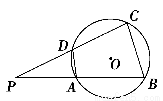
如图所示,已知PA与⊙O相切,A为切点,PBC为割线,CD∥AP,AD与BC相交于点E,F为CE上一点,且DE2=EF·EC.
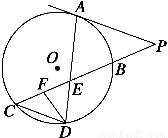
(1)求证:∠P=∠EDF;
(2)求证:CE·EB=EF·EP;
(3)若CE∶BE=3∶2,DE=6,EF=4,求PA的长.
(1) (2)见解析 (3) 
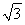
【解析】
(1)证明 ∵DE2=EF·EC,∴DE∶CE=EF∶ED.
∵∠DEF是公共角,∴△DEF∽△CED.
∴∠EDF=∠C.
∵CD∥AP,∴∠C=∠P.
∴∠P=∠EDF.
(2)证明 ∵∠P=∠EDF,∠DEF=∠PEA,
∴△DEF∽△PEA.
∴DE∶PE=EF∶EA.即EF·EP=DE·EA.
∵AD、BC相交于点E,
∴DE·EA=CE·EB.∴CE·EB=EF·EP.
(3)解 ∵DE2=EF·EC,DE=6,EF=4,∴EC=9.
∵CE∶BE=3∶2,∴BE=6.
∵CE·EB=EF·EP,∴9×6=4×EP.
解得:EP=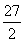 .
.
∴PB=PE-BE=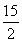 ,PC=PE+EC=
,PC=PE+EC= .
.
由切割线定理得:PA2=PB·PC,
∴PA2=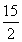 ×
× ,
,
∴PA=
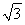 .
.

练习册系列答案
相关题目