Question

【题目】已知函数，若函数在区间内有3个零点，则实数的取值范围是_______.

Answer 1

【答案】

【解析】分析：作出函数y=f（x）和y=x+b的图象．利用两个图象的交点个数问题确定b的取值范围．

详解：若0≤x≤2，则﹣2≤x﹣2≤0，

∴f（x）=f（x﹣2）=1﹣|x﹣2+1|=1﹣|x﹣1|，

0≤x≤2．

若2≤x≤4，则0≤x﹣2≤2，

∴f（x）=f（x﹣2）=1﹣|x﹣2﹣1|=1﹣|x﹣3|，

2≤x≤4．

若4≤x≤6，则2≤x﹣2≤4，

∴f（x）=f（x﹣2）=1﹣|x﹣2﹣3|=1﹣|x﹣5|，4≤x≤6．

∴f（1）=1，f（2）=0，f（3）=1，f（5）=1，

设y=f（x）和y=x+b，则方程f（x）=x+b在区间[﹣2，6]内有3个不等实根，

等价为函数y=f（x）和y=x+b在区间[﹣2，6]内有3个不同的零点．

作出函数f（x）和y=x+b的图象，如图：

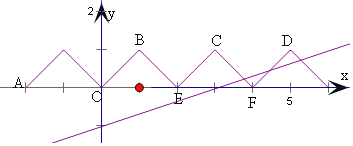
当直线经过点F（4，0）时，两个图象有2个交点，此时直线y=x+b为y=x﹣，

当直线经过点D（5，1），E（2，0）时，两个图象有3个交点；

当直线经过点O（0，0）和C（3，1）时，两个图象有3个交点，此时直线y=x+b为y=x，

当直线经过点B（1，1）和A（﹣2，0）时，两个图象有3个交点，此时直线y=x+b为y=x+，

∴要使方程f（x）=x+b，两个图象有3个交点，

在区间[﹣2，6]内有3个不等实根，

则b∈（]，

故答案为：（]．