题目内容
【题目】已知函数![]() .
.
(1)作出函数![]() 的图象;
的图象;
(2)求函数![]() 的单调区间,并指出其单调性;
的单调区间,并指出其单调性;
(3)求![]() (
(![]() )的解的个数.
)的解的个数.
【答案】(1)详见解析;(2)![]() 在
在![]() ,
,![]() 上单调递减,在
上单调递减,在![]() ,
,![]() 上单调递增;(3)当
上单调递增;(3)当![]() 时,有两个解;当
时,有两个解;当![]() 时,有三个解;当
时,有三个解;当![]() 时,有四个解;当
时,有四个解;当![]() 时,有两个解;当
时,有两个解;当![]() 时,无解.
时,无解.
【解析】
(1)借助对称性作![]() 的图象即可,
的图象即可,
(2)由图象写出函数![]() 的单调区间即可;
的单调区间即可;
(3)![]() (
(![]() )的解的个数
)的解的个数![]()
![]() 与
与![]() 图象的交点个数,作出
图象的交点个数,作出![]() 与
与![]() (
(![]() )的图象,讨论
)的图象,讨论![]() 的位置得到解的个数.
的位置得到解的个数.
(1)作![]() 的图象如下,
的图象如下,
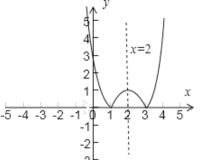 ,
,
(2)由图象可知,![]() 在
在![]() ,
,![]() 上单调递减,在
上单调递减,在![]() ,
,![]() 上单调递增;
上单调递增;
(3)![]() (
(![]() )的解的个数
)的解的个数![]()
![]() 与
与![]() 图象的交点个数,
图象的交点个数,
在同一坐标系下作![]() 与
与![]() 的图象,易知直线
的图象,易知直线![]() 有如下几种位置(虚线部分),
有如下几种位置(虚线部分),
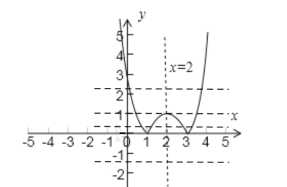
① 当![]() 时,
时,![]() 与
与![]() 的图象有两个交点,两个解;
的图象有两个交点,两个解;
② 当![]() 时,
时,![]() 与
与![]() 的图象有三个交点,三个解;
的图象有三个交点,三个解;
③ 当![]() 时,
时,![]() 与
与![]() 的图象有四个交点,四个解;
的图象有四个交点,四个解;
④ 当![]() 时,
时,![]() 与
与![]() 的图象有两个交点,两个解;
的图象有两个交点,两个解;
⑤ 当![]() 时,
时,![]() 与
与![]() 的图象有无交点,无解;
的图象有无交点,无解;

练习册系列答案
相关题目
