题目内容
【题目】已知椭圆![]() :
:![]()
![]() 的离心率为
的离心率为![]() ,且经过点
,且经过点![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)直线![]() 与椭圆
与椭圆![]() 相交于
相交于![]() ,
,![]() 两点,若
两点,若![]() ,求
,求![]() (
(![]() 为坐标原点)面积的最大值及此时直线
为坐标原点)面积的最大值及此时直线![]() 的方程.
的方程.
【答案】(1)![]() ;(2)
;(2)![]() 的最大值为
的最大值为![]() ,
,![]()
【解析】
(1)根据椭圆的离心率和经过的点,以及![]() 列方程组,解方程组求得
列方程组,解方程组求得![]() 的值,进而求得椭圆方程.(2)设出直线
的值,进而求得椭圆方程.(2)设出直线![]() 的方程
的方程![]() ,联立直线的方程和椭圆的方程,写出韦达定理,根据
,联立直线的方程和椭圆的方程,写出韦达定理,根据![]() 列方程,得到
列方程,得到![]() 的关系式.求出
的关系式.求出![]() 面积的表达式,利用配方法求得面积的最大值,进而求得直线
面积的表达式,利用配方法求得面积的最大值,进而求得直线![]() 的方程.
的方程.
(1)由题意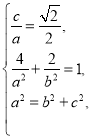 解得
解得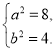 故椭圆
故椭圆![]() 的方程为
的方程为![]() .
.
(2)因为![]() ,若直线
,若直线![]() 斜率不存在,则直线
斜率不存在,则直线![]() 过原点,
过原点,
![]() ,
,![]() ,
,![]() 不能构成三角形,所以直线
不能构成三角形,所以直线![]() 的斜率一定存在,
的斜率一定存在,
设直线![]() 的方程为
的方程为![]() ,设
,设![]() ,
,![]() ,
,
由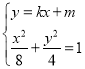 ,得
,得![]() ,
,
所以![]() ,
,![]() .
.
因为![]() ,所以
,所以![]()
![]() ,
,
即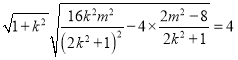 ,
,
得![]() ,显然
,显然![]() ,所以
,所以![]() .
.
又![]() ,得
,得![]() ,
,
点![]() 到直线
到直线![]() 的距离
的距离![]() .因为
.因为![]() 面积
面积![]() ,
,
所以![]()
![]()
![]() ,
,
所以当![]() 时,
时,![]() 有最大值8,即
有最大值8,即![]() 的最大值为
的最大值为![]() ,
,
此时![]() ,所以直线
,所以直线![]() 的方程为
的方程为![]() .
.

 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案【题目】为了解人们对“2019年3月在北京召开的第十三届全国人民代表大会第二次会议和政协第十三届全国委员会第二次会议”的关注度,某部门从年龄在15岁到65岁的人群中随机调查了100人,并得到如图所示的年龄频率分布直方图,在这100人中关注度非常髙的人数与年龄的统计结果如右表所示:

年龄 | 关注度非常高的人数 |
| 15 |
| 5 |
| 15 |
| 23 |
| 17 |
(Ⅰ)由频率分布直方图,估计这100人年龄的中位数和平均数;
(Ⅱ)根据以上统计数据填写下面的![]() 列联表,据此表,能否在犯错误的概率不超过
列联表,据此表,能否在犯错误的概率不超过![]() 的前提下,认为以45岁为分界点的不同人群对“两会”的关注度存在差异?
的前提下,认为以45岁为分界点的不同人群对“两会”的关注度存在差异?
(Ⅲ)按照分层抽样的方法从年龄在35岁以下的人中任选六人,再从六人中随机选两人,求两人中恰有一人年龄在25岁以下的概率是多少.
45岁以下 | 45岁以上 | 总计 | |
非常髙 | |||
一般 | |||
总计 |
参考数据:
| 0.100 | 0.050 | 0.010 | 0.001 |
| 2.706 | 3.841 | 6.635 | 10.828 |
