题目内容
已知动圆 (
( )
)
(1)当 时,求经过原点且与圆
时,求经过原点且与圆 相切的直线
相切的直线 的方程;
的方程;
(2)若圆 与圆
与圆 内切,求实数
内切,求实数 的值.
的值.
(1)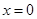 或
或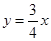 (2)
(2)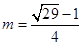
解析试题分析:(1) 时圆心为
时圆心为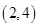 ,半径为2。当过原点的直线斜率不存在时恰好与此圆相切,此时切线方程为
,半径为2。当过原点的直线斜率不存在时恰好与此圆相切,此时切线方程为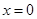 ;当过原点的直线斜率存在时设直线方程为
;当过原点的直线斜率存在时设直线方程为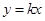 ,当直线与圆相切时圆心
,当直线与圆相切时圆心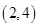 到直线
到直线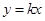 的距离等于半径2,可求得
的距离等于半径2,可求得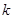 的值,从而可得切线方程。(2)圆
的值,从而可得切线方程。(2)圆 的圆心
的圆心 ,半径为
,半径为 ;圆
;圆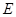 的圆心
的圆心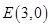 ,半径为4。当两圆内切时两圆心距等于两半径的差的绝对值,从而可得
,半径为4。当两圆内切时两圆心距等于两半径的差的绝对值,从而可得 的值。
的值。
(1)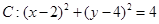
当直线 的斜率不存在时,
的斜率不存在时, 方程为
方程为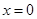 ,(3分)
,(3分)
当直线 的斜率存在时,设
的斜率存在时,设 方程为
方程为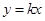 ,由题意得
,由题意得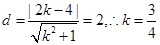
所以 方程为
方程为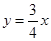 (6分)
(6分)
(2)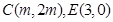 ,由题意得
,由题意得 ,(9分)
,(9分)
两边平方解得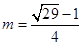
考点:1直线和圆相切;2点到线的距离;3两圆的位置关系。

练习册系列答案
相关题目
 的方程为
的方程为 ,直线
,直线
 ,设点
,设点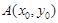 .
. 在圆
在圆 与圆
与圆 ,
, ,过点
,过点 分别交圆
分别交圆 两点,且直线
两点,且直线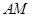 和
和 的斜率互为相反数;
的斜率互为相反数;  的值;
的值;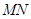 的斜率是否为定值?若是,求出该定值;若不是,说明理由.
的斜率是否为定值?若是,求出该定值;若不是,说明理由. ,圆
,圆 :
: ,过点
,过点 的动直线
的动直线 与圆
与圆 两点,线段
两点,线段 的中点为
的中点为 ,
, 为坐标原点.
为坐标原点.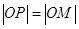 时,求
时,求 的面积
的面积 .
. 有公共点的概率.
有公共点的概率. (a>b>0,a,b为常数),动圆C1:x2+y2=t12,b<t1<a.点A1,A2分别为C0的左,右顶点,C1与C0相交于A,B,C,D四点.
(a>b>0,a,b为常数),动圆C1:x2+y2=t12,b<t1<a.点A1,A2分别为C0的左,右顶点,C1与C0相交于A,B,C,D四点.
 上,求圆C的方程。
上,求圆C的方程。 与已知圆
与已知圆 的交点,且在两坐标轴上的四个截距之和为8的圆的方程。
的交点,且在两坐标轴上的四个截距之和为8的圆的方程。 ,设点
,设点 是直线
是直线 上的两点,它们的横坐标分别是
上的两点,它们的横坐标分别是 ,点
,点 在线段
在线段 上,过
上,过 的切线
的切线 ,切点为
,切点为 .
. ,求直线
,求直线 三点的圆的圆心是
三点的圆的圆心是 ,求线段
,求线段 (
( 为坐标原点)长的最小值
为坐标原点)长的最小值 .
. 与圆
与圆 :
: 相交于
相交于 两点,若点M在圆
两点,若点M在圆 (
( 为坐标原点),则实数
为坐标原点),则实数 = ▲ .
= ▲ .