题目内容
已知：圆C过点A（6,0），B（1,5）且圆心在直线
上，求圆C的方程。
.
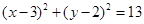解析试题分析：由圆C过A和B点，得到AB为圆C的弦，求出线段AB垂直平分线的方程，根据垂径定理得到圆心C在此方程上，方法是利用中点坐标公式求出线段AB的中点，根据直线AB的斜率，利用两直线垂直时斜率的乘积为-1求出线段AB垂直平分线的斜率，由求出的中点坐标和斜率写出线段AB垂直平分线的方程，与直线l联立组成方程组，求出方程组的解即可确定出圆心C的坐标，然后再根据两点间的距离公式求出|AC|的长即为圆C的半径，由圆心和半径写出圆C的标准方程即可．
解法1：设所求圆的方程为
。由题意可得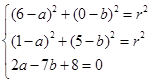
,
解得：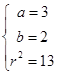
所以求圆C的方程为.
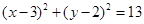解法2：求出AB垂直平分线方程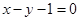
联立方程组
求出半径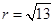
,写出圆C的方程为.
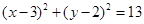考点：此题考查了中点坐标公式，两直线垂直时斜率满足的关系，垂径定理及两点间的距离公式，理解圆中弦的垂直平分线一定过圆心是解本题的关键．
练习册系列答案
云南师大附小一线名师提优作业系列答案
相关题目
中，曲线
的参数方程为
，（其中
为参数，
），在极坐标系（以坐标原点
为极点，以
轴非负半轴为极轴）中，曲线
的极坐标方程为
．
和
，求曲线
（
）
时，求经过原点且与圆
相切的直线
的方程；
内切，求实数
的值.
中，点
，直线
．设圆
的半径为
，圆心在
上．
上，过点
作圆
，使
，求圆心
的取值范围．
上，与
轴相切，且被直线
截得的弦长为
的圆的方程．
为何值时，曲线C表示圆；
交于M、N两点，且
，求
与圆
交于
，
两点，是否存在实数
为直径的圆过原点，若存在，求出实数
满足：
.
取得最小值时，圆的方程．
)作圆O:x2+y2=r2(r>0)的切线,切点为D,且|QD|=4.
=
+
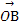,求|
是
的外接圆，过点C的切线交
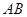的延长线于点
，
，
.则
的长为 ；
的长为 ．