题目内容
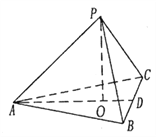
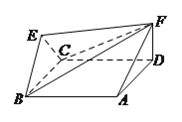
【题目】已知点R（x0 ， y0）在D：y2=2px上，以R为切点的D的切线的斜率为 
，过Γ外一点A（不在x轴上）作Γ的切线AB、AC，点B、C为切点，作平行于BC的切线MN（切点为D），点M、N分别是与AB、AC的交点（如图）．
（1）用B、C的纵坐标s、t表示直线BC的斜率；
（2）设三角形△ABC面积为S，若将由过Γ外一点的两条切线及第三条切线（平行于两切线切点的连线）围成的三角形叫做“切线三角形”，如△AMN，再由M、N作“切线三角形”，并依这样的方法不断作切线三角形…，试利用“切线三角形”的面积和计算由抛物线及BC所围成的阴影部分的面积T．
【答案】
（1）
解：设切线方程为y﹣y0= 
（x﹣x0），
kBC= 
= 
（2）
解：设D（μ，v），则MN∥BC，
∴ 
= ，（s，t为B，C的纵坐标），
v= 
D（ 
， ），
设A（a，b）利用切线方程得：
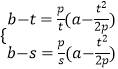即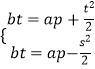 
，两式相减得：
b= ，a= 
，A（ ， ），
由前面计算可知：AD平行于横轴，可得yE= ，
BC：y﹣t= （x﹣ 
），将yE= ，代入xE= 
，
由xA+xE= + = 
=2xD，
所以D为AE的中点；
设：S△AMN=R，由上可知R= 
S△ABC= 
，
由M，N确定的确定的切线三角形的面积为 × 
= 
，
后一个切线三角形的面积是前一切线三角形面积的 
，
由此继续下去可得算式：
S△ABC=S=T+R+2 +4 
+8 
+…+，
=T+R+ 
+ 
+ +…，
∴T=S﹣ 
=S﹣ 
R= 
S
【解析】（1）根据题意可知设出直线方程，由切线斜率的定义即可表示出直线BC的斜率；（2）求得切线的斜率，可得D的坐标，求得直线BC的方程，运用中点坐标公式可得A关于D的对称点在直线BC上，求得D为AE的中点，根据MN为三角形ABC的中位线，且E为BC的中点，D为MN的中点，求得三角形ABC的面积，再由三角形的面积之比与对应边的比的关系，可得由抛物线外作出的“切线三角形”的面积构成以 S为首项， 为公比的等比数列，运用无穷递缩等比数列的求和公式，可得所有面积和，即可得到所求面积T．
