题目内容
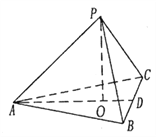
【题目】在三棱锥![]() 中,
中, ![]() ,
, ![]() 为
为![]() 的中点,
的中点, ![]() 平面
平面![]() ,垂足
,垂足![]() 落在线段
落在线段![]() 上,已知
上,已知![]() .
.
(1)证明: ![]() ;
;
(2)在线段![]() 上是否存在一点
上是否存在一点![]() ,使得二面角
,使得二面角![]() 为直二面角?若存在,求出
为直二面角?若存在,求出![]() 的长;若不存在,请说明理由.
的长;若不存在,请说明理由.
【答案】(1)证明见解析;(2)答案见解析.
【解析】试题分析:⑴对于法一,易得![]() 因为
因为![]() 平面
平面![]() ,推导出
,推导出![]() ,再推导出
,再推导出![]() 平面
平面![]() ,即可得到答案;对于法二,以
,即可得到答案;对于法二,以![]() 为原点,分别以过
为原点,分别以过![]() 点与
点与![]() 共线同向的向量,
共线同向的向量, ![]() ,
, ![]() 方向上的单位向量为单位正交基建立空间直角坐标系
方向上的单位向量为单位正交基建立空间直角坐标系![]() ,易求得几何体中各个顶点的坐标,求出
,易求得几何体中各个顶点的坐标,求出![]() ,
, ![]() 的坐标,要证明
的坐标,要证明![]() ,即证明
,即证明![]()
⑵要求满足条件使得二面角![]() 为直二面角的点
为直二面角的点![]() ,即求平面
,即求平面![]() 的法向量和平面
的法向量和平面![]() 的法向量互相垂直,由此求出点
的法向量互相垂直,由此求出点![]() 的坐标,然后根据空间两点之间的距离公式即可求出
的坐标,然后根据空间两点之间的距离公式即可求出![]() 的长;
的长;
解析:(1)法一:∵![]() ,
, ![]() 为
为![]() 的中点,
的中点,
∴![]() ,
,
∵![]() 平面
平面![]() ,
,
∴![]() ,
,
∵垂足![]() 落在线段
落在线段![]() 上,
上,
∴![]() 平面
平面![]() ,
,
∴![]() .
.
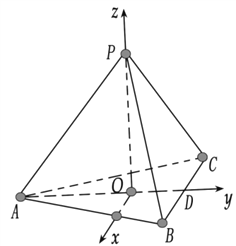
法二:如图,以![]() 为原点,分别以过
为原点,分别以过![]() 点与
点与![]() 共线同向的向量,
共线同向的向量, ![]() ,
, ![]() 方向上的单位向量为单位正交基建立空间直角坐标系
方向上的单位向量为单位正交基建立空间直角坐标系![]() ,则
,则![]()
![]()
∴![]()
∴![]()
∴![]()
(2)假设![]() 点存在,设
点存在,设![]() ,
, ![]() ,则
,则![]() ,
,
∴![]() ,
,
∴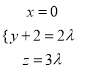 ,
,
∴![]() ,
,
∴![]()
设平面![]() 的法向量为
的法向量为![]() ,平面
,平面![]() 的法向量为
的法向量为![]()
由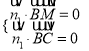 得
得![]() ,
,
令![]() ,可得
,可得![]() ,
,
由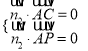 得
得![]() ,
,
令![]() ,可得
,可得![]() ,
,
若二面角![]() 为直二面角,则
为直二面角,则![]() ,得
,得![]() ,
,
解得![]() ,∴
,∴![]()
故线段![]() 上是否存在一点
上是否存在一点![]() ,满足题意,
,满足题意, ![]() 的长为
的长为![]() .
.

练习册系列答案
相关题目