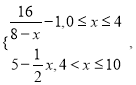题目内容
【题目】设{an}是等比数列,公比为q(q>0且q≠1),4a1 , 3a2 , 2a3成等差数列,且它的前4项和为S4=15.
(1)求{an}通项公式;
(2)令bn=an+2n(n=1,2,3…),求{bn}的前n项和.
【答案】
(1)解:∵4a1,3a2,2a3成等差数列,
∴2×3a2=4a1+2a3,
又∵数列{an}是等比数列,
∴6a1q=4a1+2 ![]() ,即q2﹣3q+2=0,
,即q2﹣3q+2=0,
解得:q=2或q=1(舍),
又∵S4=15,
∴ ![]() =15,即a1=1,
=15,即a1=1,
∴数列{an}是首项为1、公比为2的等比数列,
∴数列{an}通项公式an=2n﹣1
(2)解:由(1)可知bn=2n﹣1+2n(n=1,2,3…),
∴数列{bn}的前n项和为 ![]() +2
+2 ![]() =2n+n2+n﹣1
=2n+n2+n﹣1
【解析】(1)通过4a1 , 3a2 , 2a3成等差数列,利用首项、公比表示出前三项计算可知公比为2,利用前四项和计算可知首项,进而可得通项公式;(2)通过(1)可知bn=2n﹣1+2n,进而利用分组法求和即可.
【考点精析】解答此题的关键在于理解数列的前n项和的相关知识,掌握数列{an}的前n项和sn与通项an的关系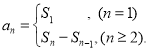 ,以及对数列的通项公式的理解,了解如果数列an的第n项与n之间的关系可以用一个公式表示,那么这个公式就叫这个数列的通项公式.
,以及对数列的通项公式的理解,了解如果数列an的第n项与n之间的关系可以用一个公式表示,那么这个公式就叫这个数列的通项公式.

【题目】《城市规划管理意见》中提出“新建住宅原则上不再建设封闭住宅小区,已建成的住宅小区和单位大院逐步打开”,此消息在网上一石激起千层浪.各种说法不一而足,为了了解居民对“开放小区”认同与否,从[25,55]岁人群中随机抽取了n人进行问卷调查,得如下数据:
组数 | 分组 | 认同人数 | 认同人数占 |
第一组 | [25,30) | 120 | 0.6 |
第二组 | [30,35) | 195 | p |
第三组 | [35,40) | 100 | 0.5 |
第四组 | [40,45) | a | 0.4 |
第五组 | [45,50) | 30 | 0.3 |
第六组 | [50,55) | 15 | 0.3 |
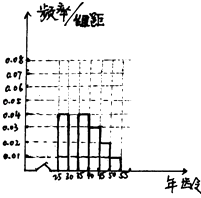
(1)完成所给频率分布直方图,并求n,a,p.
(2)若从[40,45),[45,50)两个年龄段中的“认同”人群中,按分层抽样的方法抽9人参与座谈会,然后从这9人中选2名作为组长,组长年龄在[40,45)内的人数记为ξ,求随机变量ξ的分布列和期望.