题目内容
【题目】已知双曲线![]() 的两条渐近线分别为直线
的两条渐近线分别为直线![]() ,
,![]() ,经过右焦点
,经过右焦点![]() 且垂直于
且垂直于![]() 的直线
的直线![]() 分别交
分别交![]() ,
,![]() 于
于![]() 两点,若
两点,若![]() ,
,![]() ,
,![]() 成等差数列,且
成等差数列,且![]() ,则该双曲线的离心率为( )
,则该双曲线的离心率为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】A
【解析】
由双曲线的性质可得:|AF|=b,|OA|=a,∴tan∠AOF=![]() ,∴tan∠AOB=tan2∠AOF=
,∴tan∠AOB=tan2∠AOF=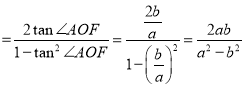 ,在直角三角形OAB中求出|AB|和|OB|,再根据等差中项列等式可得 a=2b,可得离心率.
,在直角三角形OAB中求出|AB|和|OB|,再根据等差中项列等式可得 a=2b,可得离心率.
由双曲线的性质可得:|AF|=b,|OA|=a,tan∠AOF=![]() ,
,
∴tan∠AOB=tan2∠AOF=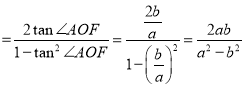
在Rt△OAB中,tan∠AOB=![]()
∴|OB|=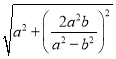 ,又|OA|,|AB|,|OB|成等差数列,∴2|AB|=|OA|+|OB|,
,又|OA|,|AB|,|OB|成等差数列,∴2|AB|=|OA|+|OB|,
∴ ,化简得:2a2﹣3ab﹣2b2=0,即(2a+b)(a﹣2b)=0,
,化简得:2a2﹣3ab﹣2b2=0,即(2a+b)(a﹣2b)=0,
∴a﹣2b=0,即a=2b,∴a2=4b2=4(c2﹣a2),5a2=4c2,∴e2=![]() .
.
故选:A.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目